D
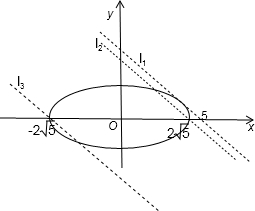
分析:根据曲线方程的特征,发现曲线表示在x轴上方的图象,画出图形,根据图形上直线的三个特殊位置,当已知直线位于直线l
1位置时,把已知直线的解析式代入椭圆方程中,消去y得到关于x的一元二次方程,由题意可知根的判别式等于0即可求出此时对应的m的值;当已知直线位于直线l
2及直线l
3的位置时,分别求出对应的m的值,写出满足题意得m的范围,综上,得到所有满足题意得m的取值范围.
解答:
解:根据曲线y=
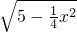
,得到5-

x
2≥0,解得:-2

≤x≤2

;y≥0,
画出曲线的图象,为椭圆在x轴上边的一部分,如图所示:
当直线y=-x+m在直线l
1的位置时,直线与椭圆相切,故只有一个交点,
把直线y=-x+m代入椭圆方程得:5x
2-8mx+4m
2-20=0,得到△=0,
即64m
2-20(4m
2-20)=0,化简得:m
2=25,解得m=5或m=-5(舍去),
则m=5时,直线与曲线只有一个公共点;
当直线y=-x+m在直线l
2位置时,直线与曲线刚好有两个交点,此时m=2

,
当直线y=-x+m在直线l3位置时,直线与曲线只有一个公共点,此时m=-2

,
则当-2

≤m<2

时,直线与曲线只有一个公共点,
综上,满足题意得m的范围是-2

≤m<2

或m=5.
故选D
点评:此题考查了直线与曲线的位置关系.根据曲线方程得出曲线表示在x轴上方的图象,进而画出图形是解本题的关键,同时本题还考查了数形结合的思想及分类讨论的思想,培养了学生发现问题,分析问题及解决问题的能力.

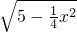 只有一个公共点,则m的取值范围是
只有一个公共点,则m的取值范围是 ≤m≤2
≤m≤2
 ≤m≤2
≤m≤2 或m=5
或m=5 解:根据曲线y=
解:根据曲线y=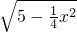 ,得到5-
,得到5- x2≥0,解得:-2
x2≥0,解得:-2 ≤x≤2
≤x≤2 ;y≥0,
;y≥0, ,
, ,
, ≤m<2
≤m<2 时,直线与曲线只有一个公共点,
时,直线与曲线只有一个公共点, ≤m<2
≤m<2 或m=5.
或m=5.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案