
分析 (1)设有x名男同学,列出方程求出男、女同学的人数分别为3、1,把3名男同学和1名女同学记为a1,a2,a3,b,由此利用列举法能求出选出的两名同学中恰有一名女同学的概率.
(2)分别求出平均数和方差,由此得到第二次同学B的实验更稳定.
解答 解:(1)设有x名男同学,则$\frac{45}{60}$=$\frac{x}{4}$,解得x=3,
∴男、女同学的人数分别为3、1,
把3名男同学和1名女同学记为a1,a2,a3,b,
则选取两名同学的基本事件有:
(a1,a2),(a1,a3),(a1,b),(a2,a1),(a2,a3),(a2,b),
(a3,a1),(a3,a2),(a3,b),(b,a1),(b,a2),(b,a3)共12种,
其中有一名女同学的有6种,
∴选出的两名同学中恰有一名女同学的概率为P=$\frac{6}{12}$=$\frac{1}{2}$.
(2)$\overline x$1=$\frac{68+70+71+72+74}{5}$=71,
$\overline x$2=$\frac{69+70+70+72+74}{5}$=71,
S12=$\frac{(68-71)2+…+(74-71)2}{5}$=4,
${{S}_{2}}^{2}$=$\frac{(69-71)2+…+(74-71)2}{5}$=3.2.
∴第二次同学B的实验更稳定.
点评 本题考查概率的求法,考查平均数、方差的求法及应用,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
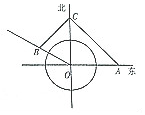 某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.
某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com