
| A、1 | B、2 | C、3 | D、4 |
科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
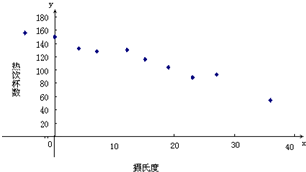 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程 |
| y |
| A、气温与热饮的销售杯数之间成正相关 | ||
| B、当天气温为2°C时,这天大约可以卖出143杯热饮 | ||
| C、当天气温为10°C时,这天恰卖出124杯热饮 | ||
D、由于x=0时,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 500 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
. |
| x |
. |
| y |
| A、①②③ | B、②③ |
| C、②③④ | D、①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、α与β相交,且交线平行于l |
| B、α与β相交,且交线垂直于l |
| C、α∥β,且l∥α |
| D、α⊥β,且l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com