
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() ,
,![]() 平面
平面![]() ,侧面
,侧面![]() 底面
底面![]() .
.
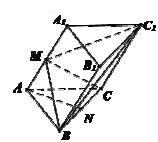
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:本题要证明线面平行以及求二面角,考虑到条件![]() ,侧面
,侧面![]() 底面
底面![]() .
.![]() ,因此取
,因此取![]() 中点
中点![]() ,有
,有![]() ,这样取
,这样取![]() 中点
中点![]() 后,易知
后,易知![]() 两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标,(1)只要求得平面
两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标,(1)只要求得平面![]() 的法向量
的法向量![]() ,然后证明
,然后证明![]() 与法向量
与法向量![]() 垂直(数量积为0)即可证明线面平行;(2)再求得
垂直(数量积为0)即可证明线面平行;(2)再求得![]() 的法向量
的法向量![]() ,由法向量
,由法向量![]() 夹角的余弦值可得二面角的余弦值(注意判断二面角是锐角还是钝角,本题是钝角).
夹角的余弦值可得二面角的余弦值(注意判断二面角是锐角还是钝角,本题是钝角).
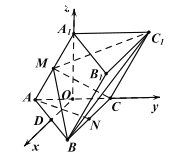
试题解析:设![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,以
中点,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]()
设![]() ,即
,即![]() ,从而
,从而![]()
显然![]() ,
,![]() ,
,
![]() ,则要使
,则要使![]() 平面
平面![]() ,则
,则![]() 且
且![]() ,
,
即![]() ,故
,故![]() ,从而点
,从而点![]() 的坐标为
的坐标为![]() ,即
,即![]() 为
为![]() 中点.
中点.
(1)设平面![]() 的法向量
的法向量![]() ,由于
,由于![]() ,
,![]() ,
,
由于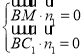 ,则
,则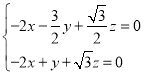 ,从而
,从而![]() ,
,
取![]()
由于![]() ,从而
,从而![]() ,从而
,从而![]() ,
,
又![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]()
(2)设平面![]() 的法向量
的法向量![]() ,由于
,由于![]() ,
,![]()
由于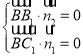 ,则
,则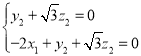 ,从而
,从而![]() ,
,
取![]()
又平面![]() 的法向量
的法向量![]()
设二面角![]() 的平面角的大小为
的平面角的大小为![]()
则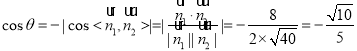
综上所述,二面角![]() 的余弦值为
的余弦值为![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】下列三句话按“三段论”模式排列顺序正确的是( )
①y =" sin" x(x ∈ R )是三角函数;② 三角函数是周期函数;
③y =" sin" x(x ∈ R )是周期函数.
A. ① ② ③ B. ② ① ③ C. ② ③ ① D. ③ ② ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下茎叶图记录了某NBA篮球队内两大中锋在六次训练中抢得篮板球数记录,由于教练一时疏忽,忘了记录乙球员其中一次的数据,在图中以X表示。
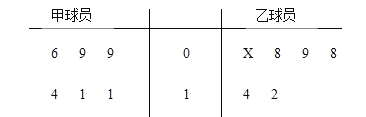
(1)如果乙球员抢得篮板球的平均数为10时,求X的值和乙球员抢得篮板球数的方差;
(2)如果您是该球队的教练在正式比赛中您会派谁上场呢?并说明理由(用数据说明)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于for x=a:b:c,下列说法正确的有( )
①当x=c时程序结束;②当x=c时,还要继续执行一次;③当b>0时,x≥a时程序结束;④当b<0时,x<a时程序结束.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,C.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面积为![]() ,求边b和c.
,求边b和c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过顶点在原点![]() ,对称轴为
,对称轴为![]() 轴的抛物线
轴的抛物线![]() 上的定点
上的定点![]() 作斜率分别为
作斜率分别为![]() 的直线,分别交抛物线
的直线,分别交抛物线![]() 于
于![]() 两点.
两点.
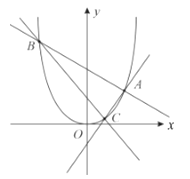
(1)求抛物线![]() 的标准方程和准线方程;
的标准方程和准线方程;
(2)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知市场上供应的灯泡中,甲厂产品占70%,乙厂占30%,甲厂产品的合格率是95%,乙厂产品的合格率是80%,则从市场上买到一个是甲厂生产的合格灯泡的概率是( )
A. 0.665 B. 0.56 C. 0.24 D. 0.028 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com