
【题目】正方体ABCD﹣A1B1C1D1中,M、N分别是CD、CC1的中点,则直线A1M与DN所成角的大小是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:以D为坐标原点,建立如图所示的空间直角坐标系;
设棱长为2,
则D(0,0,0),N(0,2,1),M(0,1,0),A1(2,0,2),![]() =(0,2,1),
=(0,2,1), ![]() =(﹣2,1,﹣2);
=(﹣2,1,﹣2);
所以 ![]()
![]() =0×(﹣2)+2×1+1×(﹣2)=0,
=0×(﹣2)+2×1+1×(﹣2)=0,
所以 ![]() ⊥
⊥ ![]() ,
,
即A1M⊥DN,异面直线A1M与DN所成的角的大小是 ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系).


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,点M,N分别为线段A1B,AC1的中点. 
(1)求证:MN∥平面BB1C1C;
(2)若D在边BC上,AD⊥DC1 , 求证:MN⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是边长为a的正方形,PB⊥平面ABCD,M、N分别是AB、PC的中点. 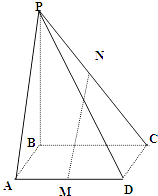
(1)求证:MN∥平面PAB;
(2)若平面PDA与平面ABCD成60°的二面角,求该四棱锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(﹣2,0),C(a,0),(a>0),设△AOB和△COD的
外接圆圆心分别为点M、N.
(Ⅰ)若⊙M与直线CD相切,求直线CD的方程;
(Ⅱ)若直线AB截⊙N所得弦长为4,求⊙N的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 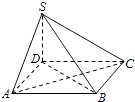
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
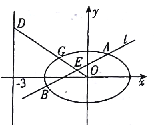
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.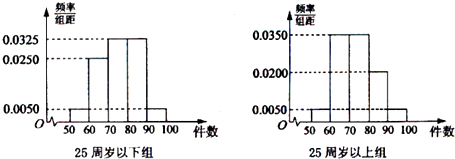
附表:
P(K2≥k) | 0.100 | 0.010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
K2= ![]() ,(其中n=a+b+c+d)
,(其中n=a+b+c+d)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | |||
25周岁以下组 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com