Question

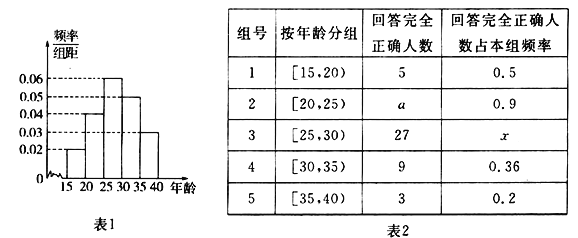
【题目】为办好省运会，计划招募各类志愿者1.2万人.为做好宣传工作，招募小组对15-40岁的人群随机抽取了100人，回答“省运会”的有关知识，根据统计结果制作了如下的统计图表1、表2：

（I）分别求出表2中的a、x的值；

（II）若在第2、3、4组回答完全正确的人中，用分层抽样的方法抽取6人，则各组应分别抽取多少人？

（III）在（II）的前提下，招募小组决定在所抽取的6人中，随机抽取2人颁发幸运奖，求获奖的2人均来自第3组的概率.

Answer 1

【答案】（1） 2）2，3，1（3）

【解析】试题分析：（1）通过频率分布直方图可求出第2，3组人数频率，从而确定其人数，然后即可求出表2中的a、x的值；

（2）根据分层抽样的性质直接计算即可；

（3）列举抽取2人所有基本事件，找出的基本事件，利用古典概型计算即可．

试题解析：

（Ⅰ）由频率直方图可知，第2，3组总人数分别为：20人，30人．

∴a=0.9×20=18（人）．．

（Ⅱ）在第2，3，4组回答完全正确的人共有54人，用分层抽样的方法抽取6人，

则各组分别抽取：

第2组： ；

第3组： 人；

第4组： 人．

∴应在第2，3，4组分别抽取2人，3人，1人．

（Ⅲ）分别记第2组的2人为A1，A2，第3组的3人为B1，B2，B3，第4组的1人为C．

则从6人中随机抽取2人的所有可能的结果为：

（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C），

（A2，B1），（A2，B2），（A2，B3），（A2，C），

（B1，B2），（B1，B3），（B1，C），

（B2，B3），（B2，C），（B3，C）

共15种情况．

获奖2人均来自第3组的有：（B1，B2），（B1，B3）（B2，B3）共3种情况．

故获奖2人均来自第3组的概率为．