【题目】已知抛物线
（
是正常数）上有两点
、
，焦点
，
甲：
；
乙：
；
丙：
；
丁：
.
以上是“直线
经过焦点”的充要条件有几个（ ）
A.
B.
C.
D.
【答案】B
【解析】
设直线
的方程为
，将直线的方程与抛物线的方程联立，利用韦达定理验证四个选项结论成立时，实数
的值，可以得出“直线经过焦点
”的充要条件的个数.
设直线的方程为，则直线交
轴于点
，且抛物线的焦点的坐标为
.
将直线的方程与抛物线的方程联立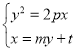
，消去得，
，
由韦达定理得
，
.
对于甲条件，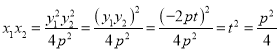
，得
，
甲条件是“直线经过焦点”的必要不充分条件；
对于乙条件，
，得
，此时，直线过抛物线的焦点，
乙条件是“直线经过焦点”的充要条件；
对于丙条件，
，即
，
解得或
，所以，丙条件是“直线经过焦点”的必要不充分条件；
对于丁条件，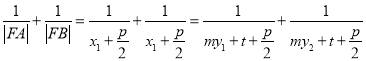
，
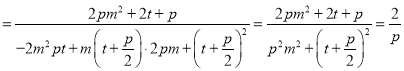化简得
，得，所以，丁条件是“直线经过焦点”的必要不充分条件.
综上所述，正确的结论只有
个，故选：B.
科目：高中数学 来源： 题型：
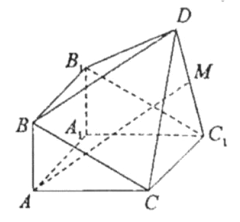
【题目】如图，由直三棱柱
和四棱锥
构成的几何体中，
，平面
平面
（I）求证：
；
（II）若M为
中点，求证：
平面
；
（III）在线段BC上（含端点）是否存在点P，使直线DP与平面所成的角为
？若存在，求
得值，若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中超足球队的后卫线上一共有7名球员，其中3人只能打中后卫，2人只能打边后卫，2人既能打中后卫又能打边后卫，主教练决定选派4名后卫上场比赛，假设可以随机选派球员．
（1）在选派的4人中至少有2人能打边后卫的概率；
（2）在选派的4人中既能打中后卫又能打边后卫的人数
的分布列与期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“珠算之父”程大为是我国明代伟大数学家，他的应用数学巨著《算法统综》的问世，标志着我国的算法由筹算到珠算转变的完成，程大位在《算法统综》中常以诗歌的形式呈现数学问题，其中有一首“竹筒容米”问题：“家有九节竹一茎，为因盛米不均平，下头三节三升九，上稍四节储三升，唯有中间两节竹，要将米数次第盛，若有先生能算法，也教算得到天明”（（注）三升九：
升，次第盛；盛米容积依次相差同一数量.）用你所学的数学知识求得中间两节的容积为（ ）
A.
升B.
升C.
升D.
升
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是（ ）
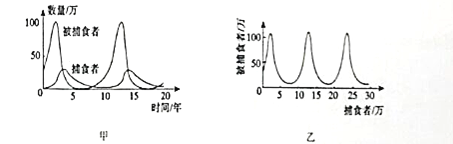
A. 捕食者和被捕食者数量与时间以
年为周期
B. 由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少
C. 捕食者和被捕食者数量之间的关系可以用图1乙描述
D. 捕食者的数量在第
年和
年之间数量在急速减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
