
【题目】设m,n∈R,若直线(m+1)x+(n+1)y﹣2=0与圆(x﹣1)2+(y﹣1)2=1相切,则m+n的取值范围是( )
A.[1﹣ ![]() ,1+
,1+ ![]() ]
]
B.(﹣∞,1﹣ ![]() ]∪[1+
]∪[1+ ![]() ,+∞)
,+∞)
C.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
D.(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞)
,+∞)
【答案】D
【解析】解:由圆的方程(x﹣1)2+(y﹣1)2=1,得到圆心坐标为(1,1),半径r=1, ∵直线(m+1)x+(n+1)y﹣2=0与圆相切,
∴圆心到直线的距离d= ![]() =1,
=1,
整理得:m+n+1=mn≤ ![]() ,
,
设m+n=x,则有x+1≤ ![]() ,即x2﹣4x﹣4≥0,
,即x2﹣4x﹣4≥0,
∵x2﹣4x﹣4=0的解为:x1=2+2 ![]() ,x2=2﹣2
,x2=2﹣2 ![]() ,
,
∴不等式变形得:(x﹣2﹣2 ![]() )(x﹣2+2
)(x﹣2+2 ![]() )≥0,
)≥0,
解得:x≥2+2 ![]() 或x≤2﹣2
或x≤2﹣2 ![]() ,
,
则m+n的取值范围为(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞).
,+∞).
故选D
由圆的标准方程找出圆心坐标和半径r,由直线与圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关系式,整理后利用基本不等式变形,设m+n=x,得到关于x的不等式,求出不等式的解集得到x的范围,即为m+n的范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知向量 ![]() ,
, ![]() ,定点
,定点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 满足
满足 ![]() ,曲线
,曲线 ![]() ,区域
,区域 ![]() ,曲线
,曲线 ![]() 与区域
与区域 ![]() 的交集为两段分离的曲线,则( )
的交集为两段分离的曲线,则( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,满足2asinA=(2b﹣ ![]() c)sinB+(2c﹣
c)sinB+(2c﹣ ![]() b)sinC. (Ⅰ)求角A的大小;
b)sinC. (Ⅰ)求角A的大小;
(Ⅱ)若a=2,b=2 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 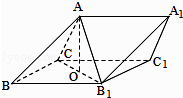
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α∈[ ![]() ,
, ![]() ],β∈[﹣
],β∈[﹣ ![]() ,0],且(α﹣
,0],且(α﹣ ![]() )3﹣sinα﹣2=0,8β3+2cos2β+1=0,则sin(
)3﹣sinα﹣2=0,8β3+2cos2β+1=0,则sin( ![]() +β)的值为( )
+β)的值为( )
A.0
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0,
(1)求l2的方程,使得:①l2与l1平行,且过点(﹣1,3); ②l2与l1垂直,且l2与两坐标轴围成的三角形面积为4;
(2)直线l1与两坐标轴分别交于A、B 两点,求三角形OAB(O为坐标原点)内切圆及外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为 ![]() 甲、
甲、 ![]() 乙 , 则下列判断正确的是( )
乙 , 则下列判断正确的是( ) 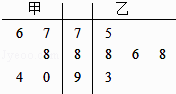
A.![]() 甲<
甲< ![]() 乙 , 甲比乙成绩稳定
乙 , 甲比乙成绩稳定
B.![]() 甲>
甲> ![]() 乙,甲比乙成绩稳定
乙,甲比乙成绩稳定
C.![]() 甲<
甲< ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
D.![]() 甲>
甲> ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com