
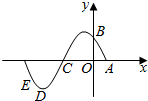
 已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )
已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
分析 根据$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,得到$OF=\frac{π}{12}$,根据三角函数的图象和性质分别求出ω 和φ的值即可得到结论.
解答  解:如图,设在点B左侧图象上的与之相邻的最高点为G,
解:如图,设在点B左侧图象上的与之相邻的最高点为G,
则由$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,知$\overrightarrow{GB}$在x轴上的投影为$\frac{π}{12}$,即|OF|=$\frac{π}{12}$,
又∵$A(\frac{π}{6},0)$,∴|AF|=$\frac{π}{12}$+$\frac{π}{6}$=$\frac{π}{4}$=$\frac{T}{4}$,
即函数的周期T=π,
∵T=$\frac{2π}{ω}$=π,∴?=2,
即f(x)=sin(2x+φ),
所以$A(\frac{π}{6},0)$,
∴sin(2×$\frac{π}{6}$+φ)=0
即$\frac{π}{3}$+φ=kπ,
即φ=kπ-$\frac{π}{3}$,
∵0<φ<π,
∴当k=1时,φ=π-$\frac{π}{3}$=$\frac{2π}{3}$,∴$f(x)=sin(2x+\frac{2π}{3})$,
∴$f(-\frac{π}{6})=sin\frac{π}{3}=\frac{{\sqrt{3}}}{2}$,
故选:B.
点评 本题主要考查三角函数的图象和性质,根据图象确定ω 和φ的值是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有$x_{\;}^2+2x+5≠0$ | B. | ?x∈R,都有$x_{\;}^2+2x+5=0$ | ||
| C. | ?x0∈R,都有$x_0^2+2{x_0}+5≠0$ | D. | ?x∉R,都有$x_{\;}^2+2x+5≠0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com