
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )
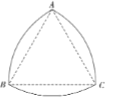
A.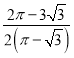 B.
B.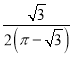
C.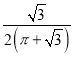 D.
D.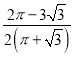
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
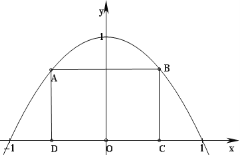
【题目】如图所示,抛物线![]() 与
与![]() 轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在
轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在![]() 轴上.已知工业用地每单位面积价值为
轴上.已知工业用地每单位面积价值为![]() 元
元![]() ,其它的三个边角地块每单位面积价值
,其它的三个边角地块每单位面积价值![]() 元.
元.
(1)求等待开垦土地的面积;
(2)如何确定点C的位置,才能使得整块土地总价值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求方程![]() 的实数解;
的实数解;
(Ⅱ)如果数列![]() 满足
满足![]() ,
,![]() (
(![]() ),是否存在实数
),是否存在实数![]() ,使得
,使得![]() 对所有的
对所有的![]() 都成立?证明你的结论.
都成立?证明你的结论.
(Ⅲ)在(Ⅱ)的条件下,设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考查某种药物预防疾病的效果,随机抽查了50只服用药的动物和50只未服用药的动得知服用药的动物中患病的比例是![]() ,未服用药的动物中患病的比例为
,未服用药的动物中患病的比例为![]() .
.
(I)根据以上数据完成下列2×2列联表:
患病 | 未患病 | 总计 | |
服用药 | |||
没服用药 | |||
总计 |
(II)能否有99%的把握认为药物有效?并说明理由.
附:
| … | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| … | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付,是指允许用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.随着信息技术的发展,手机支付越来越成为人们喜欢的支付方式.某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用手机支付的人数如下所示:(年龄单位:岁)
年龄段 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
(2)若从年龄在[55,65),[65,75]的样本中各随机选取2人进行座谈,记选中的4人中“使用手机支付”的人数为X,求随机变量X的分布列和数学期望.
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com