
【题目】已知函数![]() 满足下列条件:
满足下列条件:
①周期![]() ;②图象向左平移
;②图象向左平移![]() 个单位长度后关于
个单位长度后关于![]() 轴对称;③
轴对称;③![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)根据![]() 的周期求出
的周期求出![]() 的值,根据
的值,根据![]() 的图象平移以及
的图象平移以及![]() 的图象关于
的图象关于![]() 轴对称,求出
轴对称,求出![]() 的值,再由
的值,再由![]() 求出
求出![]() 值,解得
值,解得![]() 的表达式; (2)由
的表达式; (2)由![]() 与
与![]() 的值求出
的值求出![]() ,
, ![]() ,再根据
,再根据![]() 的范围求出
的范围求出![]() ,
, ![]() ,从而求出
,从而求出![]() 的值.
的值.
试题解析:(1)∵![]() 的周期为
的周期为![]() ,∴
,∴![]() ,又函数
,又函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,变为
个单位长度,变为![]() ,由题意,
,由题意, ![]() 的图象关于
的图象关于![]() 轴对称,∴
轴对称,∴![]() ,
, ![]() ,又
,又![]() ,∴
,∴![]() ,∴函数
,∴函数![]() ,又
,又![]() ,∴
,∴![]() ,解得
,解得![]() ,∴函数
,∴函数![]() .
.
(2)由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() .
.
点睛:本题考查五点作图法以及两角和与差的正余弦公式,属于中档题目. 利用“五点作图”求函数解析式的基本步骤:第一步:根据图象确定第一个平衡点、第二个平衡点或最高点、最低点.第二步:将“ωx+φ”作为一个整体,找到对应的值.第三步:列方程组求解.第四步:写出所求的函数解析式.第五步:反思回顾,查看关键点、易错点及答题规范.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的函数,并且满足下面三个条件:①对任意正数
上的函数,并且满足下面三个条件:①对任意正数![]() ,都有
,都有![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)如果不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+2.
(1)求f(x)单调区间
(2)求f(x)在区间[ ![]() ,3]上的最大值和最小值;
,3]上的最大值和最小值;
(3)若g(x)=f(x)﹣mx在[2,4]上是单调函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,设b>a≥0,若f(a)=f(b),则af(b)的取值范围是( )
,设b>a≥0,若f(a)=f(b),则af(b)的取值范围是( )
A.[ ![]() ,2)
,2)
B.[﹣ ![]() ,+∞)
,+∞)
C.[﹣ ![]() ,﹣
,﹣ ![]() )
)
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,且
,且![]() 为常数).
为常数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有且只有一个实根,求
上有且只有一个实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
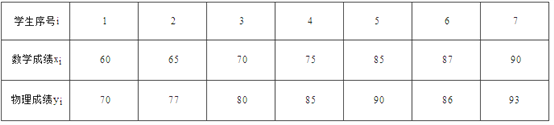
若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地有![]() ,
, ![]() 两种“共享单车”(以下简称
两种“共享单车”(以下简称![]() 型车,
型车, ![]() 型车).某学习小组7名同学调查了该地区共享单车的使用情况.
型车).某学习小组7名同学调查了该地区共享单车的使用情况.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到![]() 型车,3人租到
型车,3人租到![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到
型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到![]() 型车的概率;
型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租![]() 型车的用户中,在第4个月有
型车的用户中,在第4个月有![]() 的用户仍租
的用户仍租![]() 型车.
型车.
第3个月 第4个月 | 租用 | 租用 |
租用 |
|
|
租用 |
|
|
若认为2017年该地区租用单车情况与2016年大致相同.已知2017年3月该地区租用![]() ,
,![]() 两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com