
【题目】设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
【答案】(1)f(1)=2,f(2)=3,f(3)=4;(2)f (n)=n+1.
【解析】试题分析:(1)利用已知的表达式,通过![]() ,直接求
,直接求![]() ,利用函数的单调性以及
,利用函数的单调性以及![]() ,即可求出
,即可求出![]() 的值;(2)利用函数的单调性及数学归纳法,推出
的值;(2)利用函数的单调性及数学归纳法,推出![]() ,又
,又![]() ,然后求出
,然后求出![]() 的表达式 .
的表达式 .
试题解析:(1)因为f(1)f(4)=f(4)+f(4),所以5 f(1)=10,则f(1)=2.
因为f(n)是单调增函数
所以2=f(1)<f(2)<f(3)<f(4)=5.
因为f(n)∈Z,所以f(2)=3,f(3)=4.
(2)解:由(1)可猜想f (n)=n+1.
证明:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z,
所以f (n+1)≥f (n)+1.
首先证明:f (n)≥n+1.
因为f (1)=2,所以n=1时,命题成立.
假设n=k(k≥1)时命题成立,即f(k)≥k+1.
则f(k+1)≥f (k)+1≥k+2,即n=k+1时,命题也成立.
综上,f (n)≥n+1.
由已知可得f (2)f (n)=f (2n)+f (n+1),而f(2)=3,f (2n)≥2n+1,
所以3 f (n)≥f (n+1)+2n+1,即f(n+1)≤3 f (n)-2n-1.
下面证明:f (n)=n+1.
因为f (1)=2,所以n=1时,命题成立.
假设n=k(k≥1)时命题成立,即f(k)=k+1,
则f(k+1)≤3f (k)-2k-1=3(k+1)-2k-1=k+2,
又f(k+1)≥k+2,所以f(k+1)=k+2.
即n=k+1时,命题也成立.
所以f (n)=n+1


科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
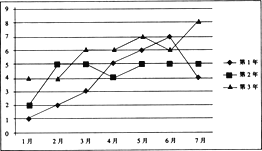
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 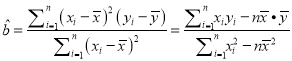 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组 ![]() .
.
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中点P(x,y),求点P落在第四象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )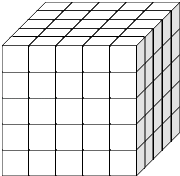
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1).当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)当![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的图象始终在直线
的图象始终在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点. 
(1)求使 ![]()
![]() 取最小值时的
取最小值时的 ![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ln x-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=3,∠ACB= ![]() .D,E分别为线段AB,BC上的点,且CD=DE=
.D,E分别为线段AB,BC上的点,且CD=DE= ![]() ,CE=2EB=2
,CE=2EB=2 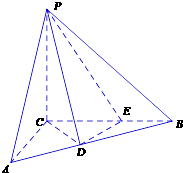
(1)证明:DE⊥平面PCD
(2)求二面角B﹣PD﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com