
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是其准线
是其准线![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() ,
,![]() 与抛物线
与抛物线![]() 相切,
相切,![]() ,
,![]() 为切点,
为切点,![]() ,
,![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
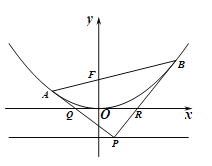
(1)求焦点![]() 的坐标,并证明直线
的坐标,并证明直线![]() 过点
过点![]() ;
;
(2)求四边形![]() 面积的最小值.
面积的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )过点
)过点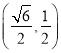 ,离心率为
,离心率为![]() .其左、右焦点分别为
.其左、右焦点分别为![]() ,
,![]() ,O为坐标原点.直线l:
,O为坐标原点.直线l:![]() 与以线段
与以线段![]() 为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若满足![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
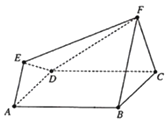
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
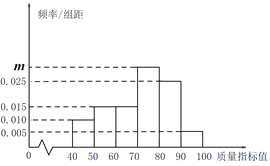
(1)求出直方图中![]() 的值;
的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com