练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（）＝（a＞0且a≠1）．

    　　（1）求f（x）的表达式，并判断奇偶性；

    　　（2）（文）若0＜a＜1，求并判断单调性．

    　　    （理）求并判断单调性．

     

    答案：
    解析：

    解：（1）令，则，∴  ，其中－1＜t＜1

    　　    即  x∈（－1，1） 

    ，所以f(x)是奇函数．

    　　（2）由解得  ∴ 

    　　     设，则

    　　（文）∵  0＜a＜1，∴  ，

    ∴  ＜0，即＜，

    ∴  f(x)递减

    　　（理）∵  当a＞1时，  又＞0お

    ∴    ∴  f(x)递增

    　      　∵  当0＜a＜1时，，

    ∴  ＜0，

    即＜ 

    ∴  f(x)递减

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：044

    已知函数f（）＝（a＞0且a≠1）．

    　　（1）求f（x）的表达式，并判断奇偶性；

    　　（2）（文）若0＜a＜1，求并判断单调性．

    　　    （理）求并判断单调性．

     

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省鹤岗一中2011－2012学年高一上学期期中考试数学理科试题 题型：013

    已知函数f(＋1)＝x＋1，则函数f(x)的解析式为

    [　　]

    A．f(x)＝x2

    B．f(x)＝x2＋1(x≥1)

    C．f(x)＝x2－2x＋2(x≥1)

    D．f(x)＝x2－2x(x≥1)

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－3)　2009－2010学年　第44期　总第200期 北师大课标 题型：044

    已知函数f(x)的定义域为A＝{x|1≤x≤7，x∈N+}，值域为B＝{0，1}．

    (1)问：这样的函数对应有多少个？

    (2)使定义域恰有4个不同元素，对应的函数值都是1，这样的函数对应有多少？

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省、兰溪一中高二下期中理科数学试卷（解析版） 题型：解答题

    （1）已知函数f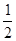(x)=x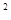－ax+(a－1)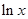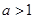，。讨论函数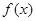的单调性；       

    （2）.已知函数f (x)=lnx，g(x)=ex．设直线l为函数 y＝f (x) 的图象上一点A(x0，f (x0))处的切线．问在区间(1，+∞)上是否存在x0，使得直线l与曲线y=g(x)也相切．若存在，这样的x0有几个？，若没有，则说明理由。

     

    查看答案和解析>>

    同步练习册答案