【答案】
分析:根据最大的系数绝对值大于等于其前一个系数绝对值;同时大于等于其后一个系数绝对值;列出不等式求出系数绝对值最大的项;据系数正负交替出现,故求系数最大的项,只需研究奇数项的系数即可;据最大的系数大于等于其前一个系数同时大于等于其后一个系数;列出不等式求出系数最大的项.
解答:解:(1)设系数绝对值最大的项是第k+1项,于是
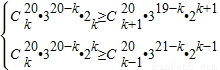
化简得
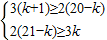
解得7 25≤k≤8 25.
所以k=8,即T9=C208312•28•x12y8是系数绝对值最大的项.
(2)由于系数为正的项为奇数项,故可设第2k-1项系数最大,于是

化简得

又k为不超过11的正整数,可得k=5,即第2×5-1=9项系数最大,T9=C208•312•28•x12•y8
点评:本题考查二项式系数的性质:中间项的二项式系数最大、考查二项展开式的通项公式、考查求系数最大项的方法.

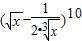 的展开式中,系数的绝对值最大的项、系数最大的项.
的展开式中,系数的绝对值最大的项、系数最大的项.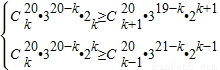 化简得
化简得 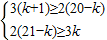 解得7 25≤k≤8 25.
解得7 25≤k≤8 25. 化简得
化简得 

