练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如图，圆O的直径AB=10，C为圆上一点，BC=6．过C作圆O的切线l，AD⊥l于点D，且交圆O于点E，求DE长．

    分析 由题意AC⊥BC，AC=$\sqrt{100-36}$=8，由已知得Rt△ACD∽Rt△ABC，从而AD=6.4，利用切割线定理、勾股定理，由此能求出DE的长．

    解答 解：由题意AC⊥BC．AC=$\sqrt{100-36}$=8，
    ∵过C作圆的切线l，过A作l的垂线AD，垂足为D，AD交圆与E，
    ∴∠ACD=∠ABC，∴Rt△ACD∽Rt△ABC，
    ∴$\frac{AC}{AB}$=$\frac{AD}{AC}$，
    ∴AD=$\frac{64}{10}$=6.4
    又DC2=DE•6.4，DC2+6.42=64，
    解得DE=3.6．

    点评 本题考查线段长的求法，是中档题，解题时要认真审题，注意弦切角性质、切割线定理的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．[普通高中]设不等式x2-2ax+a+2≤0的解集为非空数集M，且M⊆[1，4]，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．不等式-x2-x+2＜0的解集为（　　）
    A．{x|x＜-2或 x＞1 }B．{x|-2＜x＜1 }C．{x|x＜-1 或x＞2 }D．{x|-1＜x＜2 }

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．如图，在斜三棱柱ABC-A1B1C1中，侧面ACC1A1与侧面CBB1C1都是菱形，∠ACC1=∠CC1B1=60°，AC=2．
    （1）求证：AB1⊥CC1；
    （2）若$A{B_1}=\sqrt{6}$，求二面角C-AB1-A1的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=ax-lnx有极小值1+ln2
    （Ⅰ）求实数a的值；
    （Ⅱ）设g（x）=3x-3lnx-1-f（x），讨论g（x）单调性；
    （Ⅲ）若0＜x1＜x2，求证：$\frac{{x}_{1}-{x}_{2}}{ln{x}_{1}-ln{x}_{2}}$＜2x2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

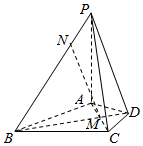    9．在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=4，AB=4$\sqrt{3}$，∠CDA=120°，点N在线段PB上，且PN=2．
    （1）求证：BD⊥PC；
    （2）求证：MN∥平面PDC；
    （3）求二面角A-PC-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=x2-（-1）n2alnx（n∈Z，a＞0）．
    （Ⅰ）求函数f（x）的极值；
    （Ⅱ）若n=2016，且函数y=2ax-f（x）有唯一零点x0，求x0与a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．如图，AB切⊙O于点B，点G为AB的中点，过G作⊙O的割线交⊙O于点C、D，连接AC并延长交⊙O于点E，连接AD并交⊙O于点F，求证：EF∥AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．函数y=cos2x+3sinx的值域是（　　）
    A．$[{-4，\frac{17}{8}}]$B．$（-∞，-4）∪（\frac{17}{8}，+∞）$C．[-4，4]D．（-∞，-4）∪（4，+∞）

    查看答案和解析>>

    同步练习册答案