
分析 ①根据两个函数的定义域相同,对应关系也相同,判断它们是否为同一函数;
②根据函数f(x-1)的定义域求出f(x)的定义域,再求函数f(3x2)的定义域即可;
③根据复合函数的单调性,判断函数y=log2(x2+2x-3)的单调区间即可.
解答 解:对于①,函数y=$\sqrt{{x}^{2}}$=|x|(x∈R),和y=($\sqrt{x}$)2=x(x≥0)的定义域不同,
对应关系也不同,∴不是同一函数,命题①错误;
对于②,函数f(x-1)的定义域为[1,2],
即x∈[1,2],∴x-1∈[0,1],
∴f(x)的定义域是[0,1];
令0≤3x2≤1,即0≤x2≤$\frac{1}{3}$,
解得-$\frac{\sqrt{3}}{3}$≤x≤$\frac{\sqrt{3}}{3}$,
∴函数f(3x2)的定义域为[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$],命题②错误;
对于③,∵x2+2x-3>0,即(x+3)(x-1)>0,
解得x<-3或x>1,
∴函数y=log2(x2+2x-3)的递增区间是(1,+∞),命题③错误;
综上,正确的命题个数为0.
故答案为:0.
点评 不同考查了判断两个函数是否为同一函数的问题,也考查了求函数的定义域以及判断复合函数的单调性问题,是综合性题目.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
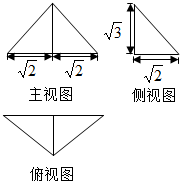 已知几何体的三视图如图所示,则该几何体的表面积为( )
已知几何体的三视图如图所示,则该几何体的表面积为( )| A. | 4+$\sqrt{6}$ | B. | 6+$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+$\sqrt{6}$ | D. | 2+2$\sqrt{3}$+$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4或-4或5 | B. | 4或-4 | C. | -4或5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (-2,2) | C. | $[-2,\sqrt{3})∪({\sqrt{3},2}]$ | D. | $(-2,\sqrt{3})∪(\sqrt{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $[0,\frac{1}{2})$ | C. | $(0,\frac{1}{2}]$ | D. | $[\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com