
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 的增区间为
的增区间为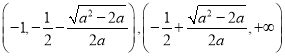 ,减区间为
,减区间为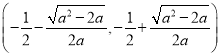 ,当
,当![]() 时,
时,![]() 的增区间为
的增区间为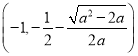 ,减区间为
,减区间为 ;(2)
;(2)![]()
【解析】
(1)求出导函数![]() ,分类讨论分子二次函数的根的情况即可得解;
,分类讨论分子二次函数的根的情况即可得解;
(2)结合(1)得出最大值![]() ,构造函数
,构造函数![]() ,结合单调性求解.
,结合单调性求解.
(1)![]()
![]() ,
,
考虑![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,记
时,记![]() 的两根
的两根![]() ,
,
结合![]() 可得:两根属于
可得:两根属于![]() ,
,
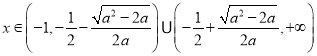 时,
时,![]() ,
,
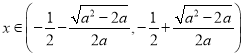 时,
时,![]() ,
,
![]() 的增区间为
的增区间为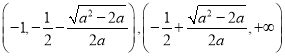 ,减区间为
,减区间为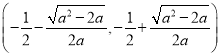 ,
,
当![]() 时,
时,![]() 开口向下,结合
开口向下,结合![]() 可得:
可得:
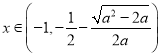 时,
时,![]() ,
,
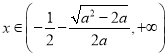 时,
时,![]() ,
,
![]() 的增区间为
的增区间为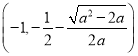 ,减区间为
,减区间为 ,
,
综上所述:当![]() 时,
时,![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 的增区间为
的增区间为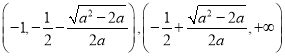 ,减区间为
,减区间为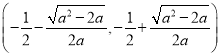 ,当
,当![]() 时,
时,![]() 的增区间为
的增区间为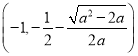 ,减区间为
,减区间为 ;
;
(2)当![]() 时,当
时,当![]() 时,
时,![]() ,
,
所以![]() ,
,
不满足![]() 对任意
对任意![]() 恒成立,
恒成立,
当![]() 时,结合(1),
时,结合(1),![]() 的增区间为
的增区间为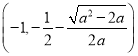 ,减区间为
,减区间为 ,
,
![]() 开口向下,结合
开口向下,结合![]() 可得:
可得:![]()
![]() 是方程
是方程![]() 的根,所以
的根,所以![]() ,
,
所以![]() ,
,
由题![]()
令![]() ,
,
![]() ,
,
易得![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,且
单调递增,且![]()
![]() ,即
,即![]() ,
,
所以![]() ,
,![]()
![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】设集合![]() 的元素均为实数,若对任意
的元素均为实数,若对任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 且
且![]() ,则称元素个数最少的
,则称元素个数最少的![]() 和
和![]() 为
为![]() 的“孪生集”;称
的“孪生集”;称![]() 的“孪生集”的“孪生集”为
的“孪生集”的“孪生集”为![]() 的“2级孪生集”;称
的“2级孪生集”;称![]() 的“2级孪生集”的“孪生集”为
的“2级孪生集”的“孪生集”为![]() 的“3级孪生集”,依此类推……
的“3级孪生集”,依此类推……
(1)设![]() ,直接写出集合
,直接写出集合![]() 的“孪生集”;
的“孪生集”;
(2)设元素个数为![]() 的集合
的集合![]() 的“孪生集”分别为
的“孪生集”分别为![]() 和
和![]() ,若使集合
,若使集合![]() 中元素个数最少且所有元素之和为2,证明:
中元素个数最少且所有元素之和为2,证明:![]() 中所有元素之和为
中所有元素之和为![]() ;
;
(3)若![]() ,请直接写出
,请直接写出![]() 的“
的“![]() 级孪生集”的个数,及
级孪生集”的个数,及![]() 所有“
所有“![]() 级孪生集”的并集
级孪生集”的并集![]() 的元素个数.
的元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.15),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65],并绘制出频率分布直方图,如图所示是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.

(1)求这次铅球投掷成绩合格的人数;
(2)你认为这次铅球投掷的同学的成绩的中位数在第几组?请说明理由;
(3)若参加这次铅球投掷的学生中,有5人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加相关部门组织的经验交流会,已知a、b 两位同学的成绩均为优秀,求a、b 两位同学中至少有1人被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右顶点为
的右顶点为![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于另一点
交于另一点![]() ,与右准线交于点
,与右准线交于点![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
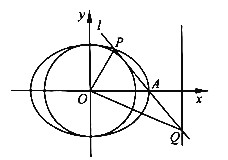
(1)用![]() 表示椭圆
表示椭圆![]() 的离心率;
的离心率;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有10位外国人,其中关注此次大阅兵的有8位,若从这10位外国人中任意选取3位做一次采访,则被采访者中至少有2位关注此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com