
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
【答案】(1)该单位月处理量为400吨时,才能使每吨的平均处理成本最低,最低成本为200元/吨;(2)该单位每月不获利,需要国家每月至少补贴40000元才能不亏损.
【解析】
(1)根据已知得平均处理成本为![]() ,得到关系式后利用基本不等式求得平均处理成本的最小值,并根据基本不等式等号成立条件求得每月处理量;(2)获利
,得到关系式后利用基本不等式求得平均处理成本的最小值,并根据基本不等式等号成立条件求得每月处理量;(2)获利![]() ,根据二次函数图象可求得
,根据二次函数图象可求得![]() ,可知不获利,同时求得国家至少补贴
,可知不获利,同时求得国家至少补贴![]() 元.
元.
(1)由题意可知,二氧化碳每吨的平均处理成本为:
![]()
当且仅当![]() ,即
,即![]() 时取等号
时取等号
![]() 月处理量为
月处理量为![]() 吨时,才能使每吨的平均处理成本最低,最低成本为
吨时,才能使每吨的平均处理成本最低,最低成本为![]() 元/吨
元/吨
(2)不获利
设该单位每月获利为![]() 元
元
![]()
![]()
![]()
故该单位每月不获利,需要国家每月至少补贴![]() 元才能不亏损
元才能不亏损


科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点,点
的一个三等分点,点![]() 是线段
是线段![]() 上的一个动点,且
上的一个动点,且![]() .如图,将
.如图,将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
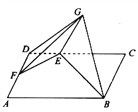
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,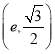 在椭圆
在椭圆![]() 上,其中
上,其中![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为椭圆的焦点,直线
为椭圆的焦点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解堵车现象,解决堵车问题,银川市交警队调查了甲乙两个路口的车流量,在2019年6月随机选取了14天,统计每天上午7:30-9:00早高峰时段各自的车流量(单位:百辆)得到如图所示的茎叶图,根据茎叶图回答以下问题.

(1)甲乙两个路口的车流量的中位数分别是多少?
(2)试计算甲乙两个路口的车流量在![]() 之间的频率.
之间的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求续驶里程在![]() 的车辆数;
的车辆数;
(2)求续驶里程的平均数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样的一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”.其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问此人第2天走的路程为
A. 24里 B. 48里 C. 72里 D. 96里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发100个红包,每个红包金额为x元,![]() .已知在每轮游戏中所产生的100个红包金额的频率分布直方图如图所示.
.已知在每轮游戏中所产生的100个红包金额的频率分布直方图如图所示.

(1)求a的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在[1,2)的红包个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员进行射击训练,前三次射击在靶上的着弹点![]() 刚好是边长为
刚好是边长为![]() 的等边三角形的三个顶点.
的等边三角形的三个顶点.

(Ⅰ)第四次射击时,该运动员瞄准![]() 区域射击(不会打到
区域射击(不会打到![]() 外),则此次射击的着弹点距
外),则此次射击的着弹点距![]() 的距离都超过
的距离都超过![]() 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间![]() 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间![]() 内.现从这
内.现从这![]() 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为![]() 和
和![]() )进行技术分析.求事件“
)进行技术分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com