
若直线l: 与抛物线
与抛物线 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。
(1)当m=-1,c=-2时,求证:OA⊥OB;
(2)若OA⊥OB,求证:直线l恒过定点;并求出这个定点坐标。
(3)当OA⊥OB时,试问△OAB的外接圆与抛物线的准线位置关系如何?证明你的结论。
解:设A(x1,y1)、B(x2,y2),由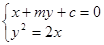 得
得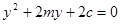
可知y1+y2=-2m y1y2=2c ∴x1+x2=2m2—2c x1x2= c2,
(1) 当m=-1,c=-2时,x1x2 +y1y2=0 所以OA⊥OB.
(2) 当OA⊥OB时,x1x2 +y1y2=0 于是c2+2c=0 ∴c=-2(c=0不合题意),此时,直线l: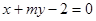 过定点(2,0).
过定点(2,0).
(3) 由题意AB的中点D(就是△OAB外接圆圆心)到原点的距离就是外接圆的半径。
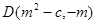 而(m2—c+
而(m2—c+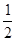 )2-[(m2—c)2+m2
]=
)2-[(m2—c)2+m2
]=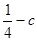 由(2)知c=-2
由(2)知c=-2
∴圆心到准线的距离大于半径,故△OAB的外接圆与抛物线的准线相离。
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011-2012年黑龙江省高二上学期期中考试文科数学 题型:解答题
若直线l: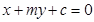 与抛物线
与抛物线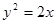 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。
(1)当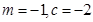 时,求证:OA⊥OB;
时,求证:OA⊥OB;
(2)若OA⊥OB,求证:直线l恒过定点;并求出这个定点坐标。
查看答案和解析>>
科目:高中数学 来源:2013届山东省高二12月月考理科数学 题型:解答题
(本小题满分12分). 若直线l: 与抛物线
与抛物线 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。
(1)当m=-1,c=-2时,求证:OA⊥OB;
(2)若OA⊥OB,求证:直线l恒过定点;并求出这个定点坐标。
(3)当OA⊥OB时,试问△OAB的外接圆与抛物线的准线位置关系如何?证明你的结论。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 与抛物线交于A,B两点.
与抛物线交于A,B两点.查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学模拟试卷1(理科)(解析版) 题型:解答题
 与抛物线交于A,B两点.
与抛物线交于A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com