已知向量a=(3,-2),b=(-2,1),c=(7,-4),试用a、b表示c.
答案:
解析:
|
答案:解:设c=ma+nb,m、n∈R
∴(7,-4)=(3m-2n,-2m+n).
∴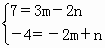 ,∴ ,∴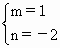 ,∴c=a-2b. ,∴c=a-2b.
分析:假设存在m、n,使c=ma+nb.由向量的坐标运算相等求m、n.
|
提示:
|
本题考查平面向量的基本定理,利用向量的相等坐标运算.由平面向量基本定理得,对于平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1、e2是平面内不共线的两个向量,一旦基底给定,λ1,λ2一定存在且唯一.
|
练习册系列答案
相关习题
科目:高中数学
来源:设计必修四数学北师版 北师版
题型:013
已知向量a=(3,4),b=(sinα,cosα),且a∥b,则tanα的值为
[ ]
A.
B.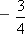
C.
D.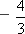
查看答案和解析>>
科目:高中数学
来源:设计必修四数学人教A版 人教A版
题型:013
已知向量a=(3,2),b=(x,4),且a∥b,则x的值为
[ ]
C.
D.
查看答案和解析>>
科目:高中数学
来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标
题型:044
已知向量a=(3,4),b=(2,-1),向量(a+mb)⊥(a-b),求m的值.
查看答案和解析>>
科目:高中数学
来源:导学大课堂选修数学2-1苏教版 苏教版
题型:044
已知向量a=(3,-2,1),b=(-2,4,0),c=(3,0,2),求a-2b+4c.
查看答案和解析>>
科目:高中数学
来源:导学大课堂必修四数学苏教版 苏教版
题型:044
已知向量a=(3,-2),b=(-2,1),c=(7,-4).试用a和b来表示c.
查看答案和解析>>
