
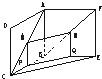
 如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.
如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE. 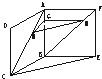 证法一:过M作MP⊥BC,NQ⊥BE,P、Q为垂足(如图),连接PQ.
证法一:过M作MP⊥BC,NQ⊥BE,P、Q为垂足(如图),连接PQ.
| ||
| 2 |
| ||
| 2 |
| BG |
| GA |
| CM |
| MA |
| BN |
| NF |


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2006年高考第一轮复习数学:9.2 直线与平面平行(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com