
【题目】已知a<﹣1,函数f(x)=|x3﹣1|+x3+ax(x∈R).
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)已知存在实数m,n(m<n≤1),对任意t0∈(m,n),总存在两个不同的t1 , t2∈(1,+∞),
使得f(t0)﹣2=f(t1)=f(t2),求证: ![]() .
.
【答案】解:(Ⅰ) ![]() ,
,
记 ![]() ,
,
则f2′(x)=6x2+a,
因为 a<﹣1则由f2′(x)=0可得x=± ![]() ,
,
(i) ![]() ,f1(x)在(﹣∞,1)上递减,
,f1(x)在(﹣∞,1)上递减,
f2(x)在[1,+∞)上递增,
所以[f(x)]min=f(1)=a+1;
(ii) ![]() ,f1(x)在(﹣∞,1)上递减,
,f1(x)在(﹣∞,1)上递减,  ,
,
所以  .
.
综上, 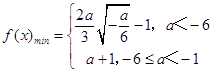 ;
;
(Ⅱ)证明:不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,
不满足题意,所以a<﹣6.
所以 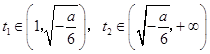 ,且
,且  ,
,
(i)a+1﹣2> ![]() ,即
,即 
即 ![]() ,解得
,解得 ![]() ,即
,即 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ;
;
(ii)a+1﹣2≤ ![]() ,即
,即 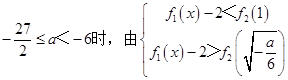 ,
,
即 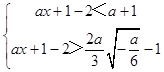 ,解得
,解得 ![]() ,
,
所以 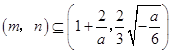 ,所以m≥1+
,所以m≥1+ ![]() ,n≤
,n≤ ![]() ,
,
所以n﹣m≤ ![]() ﹣1﹣
﹣1﹣ ![]()
令 ![]() =u∈(1,
=u∈(1, ![]() ],则
],则 ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() u﹣1+
u﹣1+ ![]() ,
,
令φ(u)= ![]() u﹣1+
u﹣1+ ![]() ,则
,则 ![]() ,
,
所以φ(u)= ![]() u﹣1+
u﹣1+ ![]() 在u∈(1,
在u∈(1, ![]() ]递增,
]递增,
所以φ(u)≤φ( ![]() )=
)= ![]() ,所以n﹣m≤φ(u)≤
,所以n﹣m≤φ(u)≤ ![]()
【解析】(Ⅰ)运用分段函数的形式写出f(x),讨论 ![]() ,
, ![]() ,判断单调性,即可得到所求最小值;(Ⅱ)不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,不满足题意,所以a<﹣6.讨论(i)a+1﹣2>
,判断单调性,即可得到所求最小值;(Ⅱ)不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,不满足题意,所以a<﹣6.讨论(i)a+1﹣2> ![]() ,(ii)a+1﹣2≤
,(ii)a+1﹣2≤ ![]() ,运用不等式的性质,求出n﹣m的不等式,即可得到证明.
,运用不等式的性质,求出n﹣m的不等式,即可得到证明.
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.

求证:(1) BE∥平面PAD;
(2) 平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=2sin2ωx+2sinωxcosωx﹣1(ω>0)的周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在[ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求与点P(3,5)关于直线l:x-3y+2=0对称的点P′的坐标.(2)已知直线l:y=-2x+6和点A(1,-1),过点A作直线l1与直线l相交于B点,且|AB|=5,求直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)已知 ![]() ,其中ai∈R,i=1,2,…10.
,其中ai∈R,i=1,2,…10.
(i)求a0+a1+a2+…+a10;
(ii)求a7 .
(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至少有一人参加,且五人均能胜任这四个岗位.
(i)若每人不准兼职,则不同的分配方案有几种?
(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过点A(1,3),B(4,2),且圆心在直线y=x﹣3上.
(Ⅰ)求圆M的方程;
(Ⅱ)若过点(﹣4,1)的直线l与圆M相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①若直线l上有无数个点不在平面α内,则l∥α;
②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;
④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程![]()
![]() 关于时间
关于时间![]() 的函数关系式分别为
的函数关系式分别为![]() ,
,![]() ,
,![]() ,
,![]() ,有以下结论:
,有以下结论:
①当![]() 时,甲走在最前面;
时,甲走在最前面;
②当![]() 时,乙走在最前面;
时,乙走在最前面;
③当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com