
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
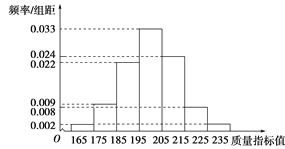
(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附: ![]() ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
【答案】(1)150(2)(ⅰ) 0.6826. (ⅱ) 68.26.
【解析】试题分析:
(1)利用题中所给的数据可得平均数![]() ,方差
,方差![]() ;
;
(2)利用正态分布的对称性可得:P(187.8<Z<212.2)=0.6826.
(3)利用(i)的结论结合题意可得![]() .
.
试题解析:
(1)抽取产品的质量指标值的样本平均数x-和样本方差s2分别为
![]() =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(2)(ⅰ)由(1)知,Z~N(200,150),从而
P(187.8<Z<212.2)=P(200-12.2<Z<200+12.2)=0.6826.
(ⅱ)由(ⅰ)知,一件产品的质量指标值位于区间(187.8,212.2)的概率为0.682 6,依题意知X~B(100,0.6826),所以E(X)=100×0.682 6=68.26.


科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xα,当x>1时,恒有f(x)<x,则α的取值范围是( )
A. (0,1) B. (-∞,1)
C. (0,+∞) D. (-∞,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 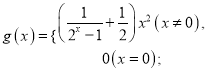
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
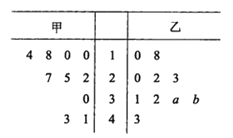
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
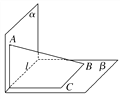
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com