
【题目】设双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() . 若点P在双曲线上,且
. 若点P在双曲线上,且![]() 为锐角三角形,则|PF1|+|PF2|的取值范围是
为锐角三角形,则|PF1|+|PF2|的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题意画出图形,不妨设P在第一象限,P点在P1与P2之间运动,求出∠PF2F1和∠F1PF2为直角时|PF1|+|PF2|的值,可得△F1PF2为锐角三角形时|PF1|+|PF2|的取值范围.
△F1PF2为锐角三角形,不妨设P在第一象限,P点在P1与P2之间运动,如图,
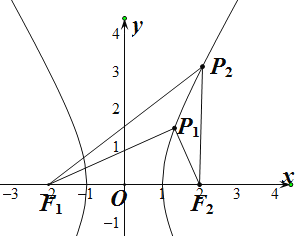
当P在P1处,∠F1P1F2为=90°,
∴S![]() =
=![]() |F1F2||y
|F1F2||y![]() |=
|=![]() |P1F1||P1F2|,
|P1F1||P1F2|,
由|P1F1|2+|P1F2|2=|F1F2|2,|P1F1|﹣|P1F2|=2,
可得|P1F1||P1F2|=6,
此时|P1F1|+|P1F2|=2![]() ,
,
当P在P2处,∠P2F1F2为=90°,x![]() =2,
=2,
易知y![]() =3,
=3,
此时|P2F1|+|P2F2|=2|P2F2|+2=8,
∴△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是(2![]() ,8),
,8),
故选:A.


科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断真假:
(1)不论![]() 取何实数,方程
取何实数,方程![]() 必有实数根;
必有实数根;
(2)所有末位数字是0或5的整数都能被5整除;
(3)某些梯形的对角线互相平分;
(4)被8整除的数能被4整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李庄村某社区电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元.
方案二:不收管理费,每度0.48元.
(1)求方案一收费![]() 元与用电量
元与用电量![]() (度)间的函数关系;
(度)间的函数关系;
(2)小李家九月份按方案一交费34元,问小李家该月用电多少度?
(3)小李家月用电量在什么范围时,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x,y)在不等式组 表示的平面区域内运动,则z=x-y的取值范围是( )
表示的平面区域内运动,则z=x-y的取值范围是( )
A. [-2,-1] B. [-2,1] C. [-1,2] D. [1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
①先将一个圆8等分(如图),再将8个等分点![]() ,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心
,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心![]() 构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球。

(1)求甲能参加音乐社团的概率;
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量![]() ,求
,求![]() 的分布列、数学期望和方差
的分布列、数学期望和方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传说《西游记》中孙悟空的“如意金箍棒”原本是东海海底的一枚“定海神针”.作为兵器,“如意金箍棒”威力巨大,且只有孙悟空能让其大小随意变化。假定孙悟空在使用“如意金箍棒”与各路妖怪打斗时,都将其变化为底面半径为4![]() 至10
至10![]() 之间的圆柱体。现假定孙悟空刚与一妖怪打斗完毕,并降伏了此妖怪,此时“如意金箍棒”的底面半径为10
之间的圆柱体。现假定孙悟空刚与一妖怪打斗完毕,并降伏了此妖怪,此时“如意金箍棒”的底面半径为10![]() ,长度为
,长度为![]() .在此基础上,孙悟空使“如意金箍棒”的底面半径以每秒1
.在此基础上,孙悟空使“如意金箍棒”的底面半径以每秒1![]() 匀速缩短,同时长度以每秒40
匀速缩短,同时长度以每秒40![]() 匀速增长,且在这一变化过程中,当“如意金箍棒”的底面半径为8
匀速增长,且在这一变化过程中,当“如意金箍棒”的底面半径为8![]() 时,其体积最大.
时,其体积最大.
(1)求在这一变化过程中,“如意金箍棒”的体积![]() 随时间
随时间![]() (秒)变化的解析式,并求出其定义域;
(秒)变化的解析式,并求出其定义域;
(2)假设在这一变化过程中,孙悟空在“如意金箍棒”体积最小时,将其定型,准备迎战下一个妖怪。求此时“如意金箍棒”的底面半径。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和抛物线
和抛物线![]() ,圆
,圆![]() 与抛物线
与抛物线![]() 的准线交于
的准线交于![]() 、
、![]() 两点,
两点,![]() 的面积为
的面积为![]() ,其中
,其中![]() 是
是![]() 的焦点.
的焦点.
(1)求抛物线![]() 的方程;
的方程;
(2)不过原点![]() 的动直线
的动直线![]() 交该抛物线于
交该抛物线于![]() ,
,![]() 两点,且满足
两点,且满足![]() ,设点
,设点![]() 为圆
为圆![]() 上任意一动点,求当动点
上任意一动点,求当动点![]() 到直线
到直线![]() 的距离最大时直线
的距离最大时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是甲、乙两名射击运动员在参赛前的训练中击中10环以上的次数统计,根据表格中的数据回答以下问题:
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
甲击中10环以上的次数 | 9 | 17 | 44 | 92 | 179 | 450 |
甲击中10环以上的频率 |
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
乙击中10环以上的次数 | 8 | 19 | 44 | 93 | 177 | 453 |
乙击中10环以上的频率 |
(1)分别计算出两位运动员击中10环以上的频率;
(2)根据(l)中的计算结果预测两位运动员在比赛时击中10环以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com