
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 处取得极值,不等式
处取得极值,不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,证明不等式
时,证明不等式![]() .
.
【答案】(1)当![]() 时函数
时函数![]() 在
在![]() 上单调递减; 当
上单调递减; 当![]() 时函数在
时函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)
上单调递增;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
试题(1)先求导,讨论导数的正负,导数正得增区间,导数负得减区间.在解不等式的过程中注意讨论![]() 的符号.(2)由(1)知函数的极值点是
的符号.(2)由(1)知函数的极值点是![]() ,则
,则![]() .可将
.可将![]() 转化为
转化为![]() ,令
,令![]() ,求导,讨论导数的符号,判断函数
,求导,讨论导数的符号,判断函数![]() 的单调性,从而求其最小值.则
的单调性,从而求其最小值.则![]() 应小于等于函数
应小于等于函数![]() 的最小值.(3)因为
的最小值.(3)因为![]() ,则
,则![]() ,
,![]() .则证明
.则证明![]() .构造函数
.构造函数![]() ,证此函数在
,证此函数在![]() 上单调递增即可.即证在
上单调递增即可.即证在![]() 上
上![]() 即可.
即可.
试题解析:(1)解![]()
![]() .
.
当![]() 时,
时,![]() ,从而
,从而![]() ,
,
函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,若
时,若![]() ,则
,则![]() ,从而
,从而![]() ,
,
若![]() ,则
,则![]() ,从而
,从而![]() ,
,
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)解 根据(1)函数的极值点是![]() ,若
,若![]() ,则
,则![]() .
.
所以![]() ,即
,即![]() ,
,
由于![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
可知![]() 为函数
为函数![]() 在
在![]() 内唯一的极小值点,也是最小值点,故
内唯一的极小值点,也是最小值点,故![]() ,
,
所以![]() 的最小值是
的最小值是![]() ,
,
故只要![]() 即可,
即可,
故![]() 的取值范围是
的取值范围是![]() .
.
(3)证明不等式![]() .
.
构造函数![]() ,
,
则![]() ,
,
可知函数在![]() 上
上![]() ,
,
即函数![]() 在
在![]() 上单调递增,由于
上单调递增,由于![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知等轴双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 在直线
在直线![]() 上,线段
上,线段![]() 的中点是坐标原点,且双曲线经过点
的中点是坐标原点,且双曲线经过点![]() .
.
(1)若已知下列所给的三个方程中有一个是等轴双曲线![]() 的方程:①
的方程:①![]() ;②
;②![]() ;③
;③![]() .请推理判断哪个是等轴双曲线
.请推理判断哪个是等轴双曲线![]() 的方程,并求出此双曲线的实轴长;
的方程,并求出此双曲线的实轴长;
(2)现要在等轴双曲线![]() 上选一处
上选一处![]() 建一座码头,向
建一座码头,向![]() 、
、![]() 两地转运货物.经测算,从
两地转运货物.经测算,从![]() 到
到![]() 、从
、从![]() 到
到![]() 修建公路的费用都是每单位长度
修建公路的费用都是每单位长度![]() 万元,则码头应建在何处,才能使修建两条公路的总费用最低?
万元,则码头应建在何处,才能使修建两条公路的总费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() ,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程;
的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
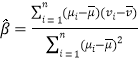 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
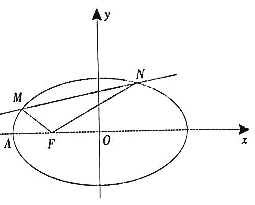
(2)如图,点![]() 分别是椭圆
分别是椭圆![]() 的左顶点、左焦点直线
的左顶点、左焦点直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() (
(![]() 都在
都在![]() 轴上方).且
轴上方).且![]() .证明:直线
.证明:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com