分析:(Ⅰ)在点(a
k,a
k2)处的切线方程为:y-a
k2=2a
k(x-a
k),当y=0时,解得
x=,所以
ak+1=,由a
1=16,知a
2=8,a
3=4,由此能推导出b
1,b
2,b
3,b
4的值.
(Ⅱ)猜想:b
n=2•3
n-1,再由数学归纳法进行证明.
(Ⅲ)由
2Tn=1+++…+,得
Tn=++…+-,所以
Tn=++…+--,
Tn=1+++…+--=
2-<2,故
Tn<.
解答:解:(Ⅰ)在点(a
k,a
k2)处的切线方程为:y-a
k2=2a
k(x-a
k),
当y=0时,解得
x=,所以
ak+1=,
又∵a
1=16,∴a
2=8,a
3=4,
a
4=2
b1==2,b2=a3+a4=6n=2时,
|b22-b1b3|<b1,
由已知b
1=2,b
2=6,得|36-2a
3|<1,
因为b
3为正整数,所以b
3=18,同理b
4=54..(4分)
(Ⅱ)由(Ⅰ)可猜想:b
n=2•3
n-1(5分)
证明:①n=1,2时,命题成立;
②假设当n=k-1与n=k(k≥2且k∈N)时成立,
即b
k=2•3
k-1,b
k-1=2•3
k-2.
于是
|bk2-bk-1bk+1|<bk-1,
整理得:
|-bk+1|<由归纳假设得:
|2•3k-bk+1|<?2•3k-<bk+1<2•3k+因为b
k+1为正整数,所以b
k+1=2•3
k即当n=k+1时命题仍成立.
综上:由知①②知对于?n∈N
*,有b
n=2•3
n-1成立(10分)
(Ⅲ)证明:由
2Tn=1+++…+③
得
Tn=++…+-④
③式减④式得
Tn=++…+-⑤
Tn=++…+--⑥
⑤式减⑥式得
Tn=1+++…+--=-1+2
(1+++…+)-+=1+2•
=+=
-1+3--+=
2-<2则
Tn<.(16分)
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.



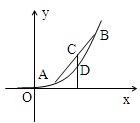 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).