
【题目】已知函数/(x![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 最小值;
最小值;
(2)若![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(3)求证:![]() .
.
【答案】(1)1;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:(I)可先求f′(x),从而判断f(x)在x∈[1,+∞)上的单调性,利用其单调性求f(x)在x∈[1,+∞)最小值;(Ⅱ)求h′(x),可得![]() 若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a﹣1)x+a<0有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,
若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a﹣1)x+a<0有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,![]() ,即
,即![]() .,再构造函数,令
.,再构造函数,令![]() ,有
,有![]() ,从而
,从而![]() ,问题可解决;(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1
,问题可解决;(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1![]() ,成立;设
,成立;设![]() 时,命题成立,即
时,命题成立,即![]() ,,再去证明n=k+1时,
,,再去证明n=k+1时,![]() 即可(需用好归纳假设).
即可(需用好归纳假设).
详解:
(1)![]() ,定义域为
,定义域为![]() .
.
∵![]()
∴![]() 在
在![]() 上是增函数.
上是增函数.
![]() .
.
(2)因为![]()
因为若![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() 有正数解.
有正数解.
即![]() 有
有![]() 有解.
有解.
①当![]() 时,明显成立.
时,明显成立.
②当![]() 时,
时,![]() 开口向下的抛物线,
开口向下的抛物线,![]() 总有
总有![]() 有解;
有解;
③当![]() 时,
时,![]() 开口向上的抛物线,即方程
开口向上的抛物线,即方程![]() 有正跟.
有正跟.
当![]() 时,
时,![]() ;
;
![]() ,解得
,解得![]() .
.
综合①②③知:![]() .
.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.
(3)(法一)根据(1)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(法二)当![]() 时,
时,![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() 时命题成立.
时命题成立.
设当![]() 时,命题成立,即
时,命题成立,即![]() .
.
∴![]() 时,
时,![]()
根据(1)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
则有![]() ,
,
即![]() 时命题也成立.
时命题也成立.
因此,由数学归纳法可知不等式成立.


科目:高中数学 来源: 题型:
【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度![]() 和对应的销售额
和对应的销售额![]() (万元)数据,如下表:
(万元)数据,如下表:
特产种类 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最满意度 |
|
|
|
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
|
|
|
![]() 求销量额
求销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() ;
;
![]() 我们约定:销量额
我们约定:销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() 的绝对值在
的绝对值在![]() 以上(含
以上(含![]() )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额![]() 关于最满意度
关于最满意度![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考数据:![]()
![]() ,
,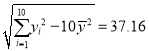 ,
,![]() ,
,![]() .
.
附:对于一组数据![]() .其回归直线方程
.其回归直线方程![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .线性相关系数
.线性相关系数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14 名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下![]() 列联表:
列联表:
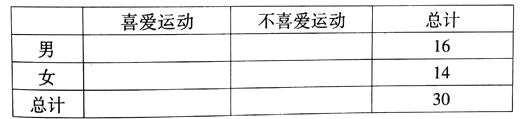
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度![]() 对亩产量
对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
残差 |
|
|
|
|
|
绘制散点图发现,可以用线性回归模型拟合亩产量![]() (吨)与海水浓度
(吨)与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求![]() 的值;
的值;
(2)统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,回归效果越好,如假设
越大,回归效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是解释变量
是解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到
(精确到![]() ),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
(附:残差![]() ,相关指数
,相关指数 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛,下面是他们的一段对话.甲说:“乙参加‘演讲’比赛”;乙说:“丙参加‘诗词’比赛”;丙说“丁参加‘演讲’比赛”;丁说:“戊参加‘诗词’比赛”;戊说:“丁参加‘诗词’比赛”.
已知这5个人中有2人参加“演讲”比赛,有3人参加“诗词”比赛,其中有2人说的不正确,且参加“演讲”的2人中只有1人说的不正确.根据以上信息,可以确定参加“演讲”比赛的学生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com