Question

15．设f（x）=log${\;}_{\frac{1}{2}}$x-a^x＞0在（0，$\frac{1}{4}$）上恒成立，a＞0且a≠1，求a范围（　　）

• A． （1，+∞）
• B． （0，1）
• C． （0，1）∪（1，16]
• D． （1，16]

Answer 1

分析 可以先画出函数$y=lo{g}_{\frac{1}{2}}x$及y=a^x的图象，然后据图加以分析，只要当$x∈（0，\frac{1}{4}）$时，前者函数图象在后者函数图象的上方即可．要注意对指数函数的底数a加以讨论解决问题．

解答 解：由$lo{g}_{\frac{1}{2}}x-{a}^{x}＞0$，得$lo{g}_{\frac{1}{2}}x＞{a}^{x}$当$x∈（0，\frac{1}{4}）$时恒成立．
当a＞1时，作出这两个函数的图象如下：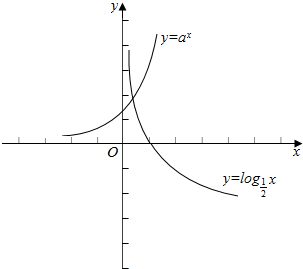

易知，当$x=\frac{1}{4}$时，对数函数图象上的点在指数函数图象上的点上方即可，即$lo{g}_{\frac{1}{2}}\frac{1}{4}≥{a}^{\frac{1}{4}}$，解得1＜a≤16；
同理，当0＜a＜1时，亦有$lo{g}_{\frac{1}{2}}\frac{1}{4}≥{a}^{\frac{1}{4}}$，解得0＜a＜1．
综上可知，所求a的范围是（0，1）∪（1，16]．
故选：C．

点评 本题主要是考查了不等式恒成立问题的解题思路，一般是转化为函数的最值问题求解，本题主要是借助于函数的图象解决问题，即也考查了数形结合的思想方法．