设集合A={x|4x-2x+2+a=0,x∈R}.
(1)若A中仅有一个元素,求实数a的取值集合B;
(2)若对于任意a∈B,不等式x2-6x<a(x-2)恒成立,求x的取值范围.
【答案】
分析:(1)令2
x=t(t>0),设f(t)=t
2-4t+a,通过换元可知:由f(t)=0在(0,+∞)上仅有一根或两相等实根,通过分类讨论利用△及其根与系数的关系即可得出;
(2)要使原不等式对任意a∈(-∞,0]∪{4}恒成立,即g(a)=(x-2)a-(x
2-6x)>0恒成立.转化为一次函数,利用其单调性只须

解出即可.
解答:解:(1)令2
x=t(t>0),设f(t)=t
2-4t+a,由f(t)=0在(0,+∞)上仅有一根或两相等实根,
①f(t)=0有两等根时,△=0⇒16-4 a=0⇒a=4.
验证:t
2-4t+4=0⇒t=2∈(0,+∞)这时x=1.
②f(t)=0有一正根和一负根时,f(0)<0⇒a<0.
③若f(0)=0,则a=0,此时4
x-2•2
x=0⇒2
x=0,(舍去),或2
x=4,∴x=2,此时A中只有一个元素.
∴实数a的取值集合为B={a|a≤0或a=4}.
(2)要使原不等式对任意a∈(-∞,0]∪{4}恒成立,即g(a)=(x-2)a-(x
2-6x)>0恒成立.
只须
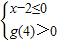
⇒
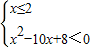
⇒5-

<x≤2.
点评:熟练掌握换元法、指数函数的单调性、一元二次方程的判别式△及根与系数的关系、一次函数的单调性等是解题的关键.

 解出即可.
解出即可.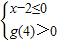 ⇒
⇒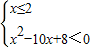 ⇒5-
⇒5- <x≤2.
<x≤2.
