
分析 (1)Sn=2an+n-3,当n=1时,a1=S1=2a1-2,解得a1.当n≥2时,利用an=Sn-Sn-1,化为:an=2an-1+1,变形为an-1=2(an-1-1),利用等比数列的定义即可证明.
(2)由(1)可得:bn=2n-1=an-1,可得an=2n-1+1.利用“错位相减法”、等比数列与等差数列的求和公式即可得出.
解答 (1)证明:∵Sn=2an+n-3,∴当n=1时,a1=S1=2a1-2,解得a1=2.
当n≥2时,an=Sn-Sn-1=2an+n-3-(2an-1+n-1-3),化为:an=2an-1+1,变形为an-1=2(an-1-1),
∵bn=an-1,∴bn=2bn-1,b1=2-1=1,
∴{bn}为等比数列,首项为1,公比为2.
(2)解:由(1)可得:bn=2n-1=an-1,∴an=2n-1+1.
∴cn=nan=n•2n-1+n.
设数列{n•2n-1}的前n项和为:An.
则An=1+2×2+3×22+…+n•2n-1,
∴2An=2+2×22+…+(n-1)•2n-1+n•2n,
∴-An=1+2+22+…+2n-1-n•2n=$\frac{{2}^{n}-1}{2-1}$-n•2n=(1-n)×2n-1,
∴An=(n-1)×2n+1.
∴数列{cn}的前n项和Tn=(n-1)×2n+1+$\frac{n(n+1)}{2}$.
点评 本题考查了递推关系、“错位相减法”、等比数列与等差数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
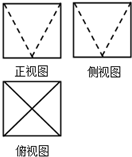 某几何体的三视图如图所示,图中的正视图、侧视图、俯视图都是边长为1的正方形,两条虚线的交点为正方形一边的中点,则该几何体的体积是( )
某几何体的三视图如图所示,图中的正视图、侧视图、俯视图都是边长为1的正方形,两条虚线的交点为正方形一边的中点,则该几何体的体积是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2018}{2019}$ | B. | $\frac{2017}{2018}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=±$\frac{\sqrt{15}}{2}$y | B. | y=±$\frac{\sqrt{15}}{2}$x | C. | x=±$\frac{\sqrt{2}}{2}$y | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>1} | B. | {x|x<-1或x>2} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个都是篮球 | B. | 至少有1个是气排球 | ||
| C. | 3个都是气排球 | D. | 至少有1个是篮球 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆 与双曲线
与双曲线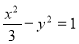 的离心率互为倒数,且直线
的离心率互为倒数,且直线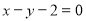 经过椭圆的右顶点.
经过椭圆的右顶点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设不过原点 的直线
的直线 与椭圆
与椭圆 交于
交于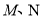 两点,且直线
两点,且直线 、
、 、
、 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△ 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com