
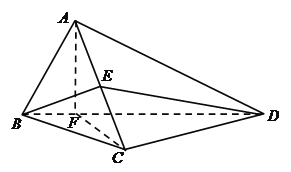
【题目】如图,在四面体![]() 中,
中,![]() ,
, ![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,四面体
,四面体![]() 的体积为2,求二面角
的体积为2,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)作Rt△![]() 斜边
斜边![]() 上的高
上的高![]() ,连结
,连结![]() ,易证
,易证![]() 平面
平面![]() ,从而得证;
,从而得证;
(2)由四面体![]() 的体积为2,
的体积为2,![]() ,得
,得![]() ,所以
,所以![]() 平面
平面![]() ,以
,以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用面的法向量求解二面角的余弦值即可.
,利用面的法向量求解二面角的余弦值即可.
详解:解法一:(1)如图,作Rt△![]() 斜边
斜边![]() 上的高
上的高![]() ,连结
,连结![]() .
.
因为![]() ,
,![]() ,所以Rt△
,所以Rt△![]() ≌Rt△
≌Rt△![]() .可得
.可得![]() .所以
.所以![]() 平面
平面![]() ,于是
,于是![]() .
.
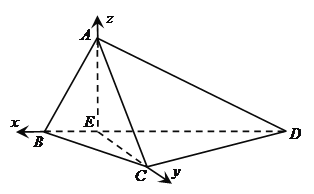
(2)在Rt△![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
, ![]() ,△
,△![]() 的面积
的面积![]() .因为
.因为![]() 平面
平面![]() ,四面体
,四面体![]() 的体积
的体积![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .则
.则![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则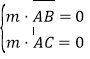 ,即
,即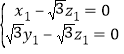 ,可取
,可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则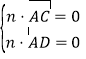 ,即
,即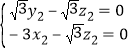 ,可取
,可取![]() .
.
因为![]() ,二面角
,二面角![]() 的平面角为钝角,所以二面角
的平面角为钝角,所以二面角![]() 的余弦值为
的余弦值为![]()
解法二:(1)因为![]() ,
,![]() ,所以Rt△
,所以Rt△![]() ≌Rt△
≌Rt△![]() .可得
.可得![]() .
.
设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,,于是
,,于是![]() .
.
(2)在Rt△![]() 中,因为
中,因为![]() ,
,![]() ,所以△
,所以△![]() 面积为
面积为![]() .设
.设![]() 到平面
到平面![]() 距离为
距离为![]() ,因为四面体
,因为四面体![]() 的体积
的体积![]() ,所以
,所以![]() .
.
在平面![]() 内过
内过![]() 作
作![]() ,垂足为
,垂足为![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() .由点到平面距离定义知
.由点到平面距离定义知![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() .因为
.因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是 ![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是 ![]() ,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望.
,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面斜坐标系![]() 中,
中,![]() ,平面上任意一点
,平面上任意一点![]() 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若![]() (其中
(其中![]() ,
,![]() 分别为与
分别为与![]() 轴,
轴,![]() 轴同方向的单位向量),则
轴同方向的单位向量),则![]() 点的斜坐标为
点的斜坐标为![]()

(1)若点![]() 在斜坐标系
在斜坐标系![]() 中的坐标为
中的坐标为![]() ,求点
,求点![]() 到原点
到原点![]() 的距离.
的距离.
(2)求以原点![]() 为圆心且半径为
为圆心且半径为![]() 的圆在斜坐标系
的圆在斜坐标系![]() 中的方程.
中的方程.
(3)在斜坐标系![]() 中,若直线
中,若直线![]() 交(2)中的圆于
交(2)中的圆于![]() 两点,则当
两点,则当![]() 为何值时,
为何值时,![]() 的面积取得最大值?并求此最大值.
的面积取得最大值?并求此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=![]() ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;
(2)若圆C1与圆C2相内切,求圆C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com