
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |
分析 根据题意和三角形的面积公式求出sinC的值,由内角的范围、特殊角的正弦值求出角C,再分别利用余弦定理求出AB的值,并利用余弦定理验证是否符合条件.
解答 解:由题意得,钝角三角形ABC,若AC=1,BC=2,且△ABC的面积为$\frac{{\sqrt{3}}}{2}$,
则$\frac{1}{2}×1×2$×sinC=$\frac{{\sqrt{3}}}{2}$,解得sinC=$\frac{{\sqrt{3}}}{2}$,
由0<C<π得,C=$\frac{π}{3}$或$\frac{2π}{3}$,
当C=$\frac{π}{3}$时,由余弦定理得:AB2=AC2+BC2-2AC•BC•cosC=1+4-2×1×$2×\frac{1}{2}$=3,AB=$\sqrt{3}$,
则A是最大角,cosA=0,则A是直角,
这与三角形是钝角三角形矛盾,
所以C=$\frac{2π}{3}$,则AB2=AC2+BC2-2AC•BC•cosC=1+4+2×1×$2×\frac{1}{2}$=7,则AB=$\sqrt{7}$,
故选:B.
点评 本题考查余弦定理及其变形,三角形的面积公式,以及特殊角的三角函数值,注意内角的范围,考查化简、计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
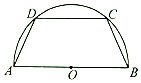 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
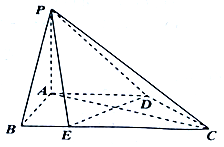 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com