
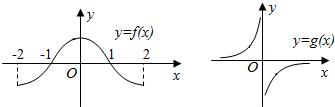
| A. | 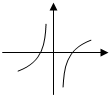 | B. |  | C. |  | D. | 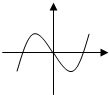 |
分析 由已知中函数y=f(x)与y=g(x)的图象我们不难分析,当函数y=f(x)•g(x)有两个零点M,N,我们可以根据函数y=f(x)与y=g(x)的图象中函数值的符号,分别讨论(-∞,M)(M,0)(0,N)(N,+∞)四个区间上函数值的符号,以确定函数的图象.
解答 解:∵y=f(x)的有两个零点,并且g(x)没有零点;
∴函数y=f(x)•g(x)也有两个零点M,N,
又∵x=0时,函数值不存在
∴y在x=0的函数值也不存在
当x∈(-∞,M)时,y<0;
当x∈(M,0)时,y>0;
当x∈(0,N)时,y<0;
当x∈(N,+∞)时,y>0;
只有A中的图象符合要求.
故选:A.
点评 要根据已知两个函数的图象,判断未知函数的图象,我们关键是要根据已知条件中的函数的图象,分析出未知函数零点的个数,及在每个区间上的符号,然后对答案中的图象逐一进行判断,然后选出符合分析结果的图象.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有两个面平行,其余各面都是平行四边形的几何体是棱柱 | |
| B. | 用一个平面去截棱锥,底面和截面之间的部分组成的几何体是棱台 | |
| C. | 用一个平面去截圆锥,截面曲线一定是圆 | |
| D. | 正方体的内切球直径是这个正方体的棱长 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com