
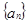 的前
的前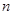 项和
项和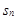 满足
满足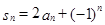 ,
,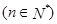
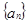 的前三项
的前三项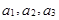
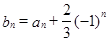 ,求证:数列
,求证:数列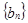 为等比数列,并指出
为等比数列,并指出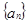 的通项公式。
的通项公式。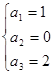 ;(Ⅱ)
;(Ⅱ)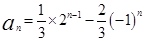 .
.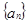 的前三项
的前三项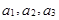 ,在
,在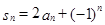 中分别令
中分别令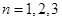 即可求出
即可求出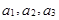 ;(Ⅱ)数列
;(Ⅱ)数列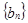 为等比数列,只需证明
为等比数列,只需证明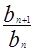 等于一个与
等于一个与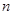 无关的常数,由
无关的常数,由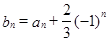 ,首先求出数列
,首先求出数列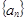 的通项公式,或递推式,由
的通项公式,或递推式,由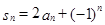 ,这是已知
,这是已知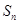 ,求
,求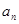 ,可利用
,可利用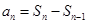 来求,即当
来求,即当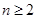 ,
,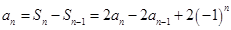 ,可得
,可得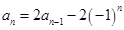 ,由
,由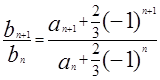 ,把
,把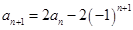 代入可得
代入可得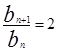 ,从而可证,求
,从而可证,求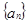 的通项公式,由
的通项公式,由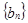 是首项为
是首项为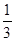 ,公比为2的等比数列,可写出
,公比为2的等比数列,可写出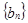 的通项公式,从而可得数列
的通项公式,从而可得数列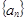 的通项公式.
的通项公式.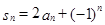 中分别令n=1,2,3得
中分别令n=1,2,3得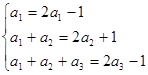 (2分) 解得
(2分) 解得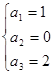 (4分)
(4分)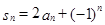 ,n≥1得
,n≥1得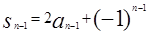 ,n≥2
,n≥2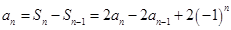 ,即
,即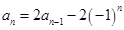 , (6分)
, (6分)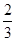 (-1)n=2an-1+
(-1)n=2an-1+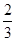 (-1)n-2(-1)n=2an-1+
(-1)n-2(-1)n=2an-1+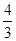 (-1)n-1
(-1)n-1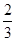 (-1)n-1](n≥2) (9分)
(-1)n-1](n≥2) (9分)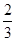 =
=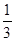
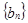 是首项为
是首项为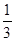 ,公比为2的等比数列. (10分)
,公比为2的等比数列. (10分)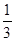 ×2n-1= an+
×2n-1= an+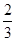 (-1)n
(-1)n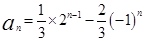 (12分)
(12分)

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com