
【题目】(1)求证:正三角形各顶点到其外接圆上任一切线的距离之和为定值;
(2)猜想空间命题“正四面体各顶点到其外接球的任一切面的距离之和为定值”是否成立?证明你的结论.注:与球只有一个公共点的平面叫做球的切面,这个公共点叫做切点,切点与球心的连线垂直于切面.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】我市正在创建全国文明城市,某高中为了解学生的创文知晓率,按分层抽样的方法从“表演社”、“演讲社”、“围棋社”三个活动小组中随机抽取了6人进行问卷调查,各活动小组人数统计如下图:


(1)从参加问卷调查的6名学生中随机抽取2名,求这2名学生来自同一小组的概率;
(2)从参加问卷调查的6名学生中随机抽取3名,用![]() 表示抽得“表演社”小组的学生人数,求
表示抽得“表演社”小组的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内接等腰梯形![]() 中,已知
中,已知![]() ,对角线
,对角线![]() 、
、![]() 交于点
交于点![]() ,且图中各条线段长均为正整数,
,且图中各条线段长均为正整数,![]() ,圆的半径
,圆的半径![]() .
.
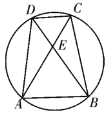
(1)求证:图中存在一个三角形,其三边长均为质数且组成等差数列;
(2)若给图中的线(包括圆、梯形、梯形的对角线)作点染色,使![]() 、
、![]() 、
、![]() 染上红色,其他点染上红蓝色之一,求证:图中存在三个同色点,两两距离相等且长度为质数.
染上红色,其他点染上红蓝色之一,求证:图中存在三个同色点,两两距离相等且长度为质数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄平县且兰高中全体师生努力下,有效进行了“一对一辅导战略”成绩提高了一倍,下列是“优秀学生”,“中等学生”,“差生”进行“一对一”前后所占比例
战略前 | 战略后 | |||||
优秀学生 | 中等学生 | 差生 | 优秀学生 | 中等学生 | 差生 | |
20% | 50% | 30% | 25% | 45% | 30% | |
则下列结论正确的是( )
A.实行“一对一”辅导战略,差生成绩并没有提高.
B.实行“一对一”辅导战略,中等生成绩反而下降了.
C.实行“一对一”辅导战略,优秀学生成绩提高了.
D.实行“一对一”辅导战略,优秀学生与中等生的成绩没有发生改变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线l过点
的焦点为F,直线l过点![]() .
.
(1)若点F到直线l的距离为![]() ,求直线l的斜率;
,求直线l的斜率;
(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com