
 的前n项和,证明对于任意给定的实数N,总可以找到一个正整数m,使得当n>m时,Sn>N.
的前n项和,证明对于任意给定的实数N,总可以找到一个正整数m,使得当n>m时,Sn>N.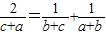 ,只须证2b2=a2+c2.因为a2,b2,c2成等差数列,所以2b2=a2+c2成立,由此能证明b+c,c+a,a+b成调和数列.
,只须证2b2=a2+c2.因为a2,b2,c2成等差数列,所以2b2=a2+c2成立,由此能证明b+c,c+a,a+b成调和数列.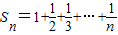 ,所以
,所以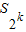 =
=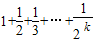 >1+
>1+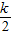 ,对于任一给定的N,欲使Sn>N,只须
,对于任一给定的N,欲使Sn>N,只须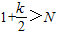 ,即k>2(N-1),由此能够证明当n>m时,Sn>N.
,即k>2(N-1),由此能够证明当n>m时,Sn>N.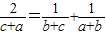
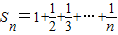
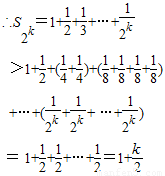
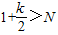 ,
,

科目:高中数学 来源: 题型:
| 1 | n |
查看答案和解析>>
科目:高中数学 来源:北京五中2007-2008学年度第一学期期中考试试卷高三数学(文科) 题型:044
如果一个数列的各项的倒数成等差数列,我们把这个数列叫做调和数列
(1)若a2,b2,c2成等差数列,证明b+c,c+a,a+b成调和数列;
(2)设Sn是调和数列![]() 的前n项和,证明对于任意给定的实数N,总可以找到一个正整数m,使得当n>m时,Sn>N
的前n项和,证明对于任意给定的实数N,总可以找到一个正整数m,使得当n>m时,Sn>N
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)设数列{an}是公方差为p的等方差数列,求an和an-1(n≥2,n∈N)的关系式;
(2)若数列{an}既是等方差数列,又是等差数列,证明该数列为常数列.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com