
【题目】如图,在△ABC中,∠B=![]() ,AB=8,点D在BC边上,且CD=2,cos∠ADC=
,AB=8,点D在BC边上,且CD=2,cos∠ADC=![]() .
.

(1)求sin ∠BAD;
(2)求BD,AC的长.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
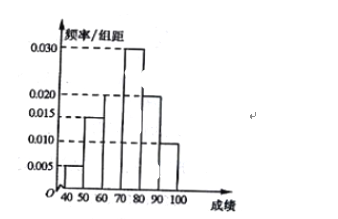
【题目】某中学举行了数学测试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(I)若该所中学共有3000名学生,试利用样本估计全校这次考试中优秀生人数;
(II)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人,试求恰好抽中1名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,且点
,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过椭圆 ![]() 上异于其顶点的任意一点
上异于其顶点的任意一点 ![]() 作圆
作圆 ![]() 的两条切线,切点分别为
的两条切线,切点分别为 ![]() (
( ![]() 不在坐标轴上),若直线
不在坐标轴上),若直线 ![]() 在
在 ![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为 ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}(n∈N*)满足:a1=1,an+1-sin2θ·an=cos 2θ·cos2nθ,其中θ∈![]() .
.
(1)当θ=![]() 时,求数列{an}的通项公式;
时,求数列{an}的通项公式;
(2)在(1)的条件下,若数列{bn}满足bn=sin![]() +cos
+cos![]() (n∈N*,n≥2),且b1=1,求证:对任意的n∈N*,1≤bn≤
(n∈N*,n≥2),且b1=1,求证:对任意的n∈N*,1≤bn≤![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为 ![]() .
.
(1)若一条直径的斜率为 ![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为 ![]() 和
和 ![]() ,它们的斜率分别为
,它们的斜率分别为 ![]() ,证明:四边形
,证明:四边形 ![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且.
,且.![]() .
.
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项的
项的![]() ;
;
(3)将数列![]() 与
与![]() 的项相间排列构成新数列
的项相间排列构成新数列![]() ,设新数列
,设新数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数n都有
,若对任意正整数n都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天时间与水深(单位:米)的关系表:
时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深 | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)请用一个函数来近似描述这个港口的水深y与时间t的函数关系;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上认为是安全的(船舶停靠时,船底只要不碰海底即可)。某船吃水深度(船底离地面的距离)为6.5米。
Ⅰ)如果该船是旅游船,1:00进港希望在同一天内安全出港,它至多能在港内停留多长时间(忽略进出港所需时间)?
Ⅱ)如果该船是货船,在2:00开始卸货,吃水深度以每小时0.5米的速度减少,由于台风等天气原因该船必须在10:00之前离开该港口,为了使卸下的货物尽可能多而且能安全驶离该港口,那么该船在什么整点时刻必须停止卸货(忽略出港所需时间)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com