
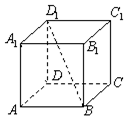
 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,分析 ①正方形ABCD-A1B1C1D1中,前后、左右两对侧面相互平行,利用面面平行的性质定理可判断四边形BFD1E是平行四边形;
②先假设四边形BFD1E是正方形,利用勾股定理可导出矛盾,从而可判断其正误;
③四边形BFD1E在底面ABCD内的投影为ABCD,是正方形,可判断其正误;
④四利用菱形的对角线互相垂直及面面垂直的性质,可判断四边形BFD1E有可能垂直于平面BB1D.
解答 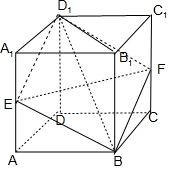 解:连接D1E、D1F、BE、BF、EF,
解:连接D1E、D1F、BE、BF、EF,
对于①,正方形ABCD-A1B1C1D1中,前后、左右两对侧面相互平行,由面面平行的性质定理可得,BE∥D1F,D1E∥BF,故四边形BFD1E一定是平行四边形,①正确;
对于②,设该正方体的边长为2,若四边形BFD1E是正方形,
则E、F分别为AA1与CC1的中点,D1E=BE且D1E⊥BE,
实际上,D1E=BE=,
BD1=2,并不满足D1E2+BE2=BD12,即D1E⊥BE不成立,故②错误;
对于③,四边形BFD1E在底面ABCD内的投影是ABCD,为正方形,故③正确;
对于④,当E和F是所在棱的中点时,易证BE=D1E,则四边形BFD1E是菱形,则EF垂直于BD1,同理四边形B1FDE也是菱形,则EF垂直于B1D,因此EF垂直于平面BB1D1D,从而平面BFD1E垂直于平面BB1D1D,即四边形BFD1E有可能垂直于平面BB1D,故④正确.
综上所述,以上结论正确的为①③④.
故答案为:①③④.
点评 本题考查命题的真假判断与应用,突出考查空间几何中面面平行、面面垂直的性质与判定,考查作图、分析与逻辑推理能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
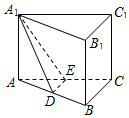 如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.
如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com