已知数列{an}的每一项都是非负实数,且对任意m,n∈N*有am+n-am-an=0或am+n-am-an=1.
又知a2=0,a3>0,a99=33.则a3= ,a10= .
【答案】
分析:本题的题意不是求通项公式,a
m+n-a
m-a
n=0或a
m+n-a
m-a
n=1这类递推式子较少见到,理解不到位很容易出现偏差,本题应当求出a
1的值,再利用a
3=a
1+a
2求出a
3,对a
10的求解需要确定范围,才能进一步求出.
解答:解:(1)由已知:a
2=a
1+a
1=0或a
2=a
1+a
1+1=0,所以2a
1=0或2a
1=0-1=-1,又因为a
n≥0,所以a
1=0;
所以a
3=a
1+a
2=0或a
3=a
1+a
2+1=1,由已知a
3>0,所以a
3=1
(2)由(1)及已知a
m+n-a
m-a
n=0或a
m+n-a
m-a
n=1,a
1=a
2=0,a
3=1可知对任意n∈N
*,a
n∈Z,a
m+n=a
m+a
n或a
m+n=a
m+a
n+1,反复利用上式可得33=a
99≥a
89+a
10≥a
79+2a
10≥…≥9a
10+3a
3=9a
10+3,所以
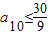
,同理可得33=a
99≤9a
10+3a
3+11
所以
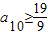
,即有
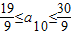
,又因为a
n∈Z,所以a
10=3.
点评:这是一道稍有难度的递推数列题目,难在打破常规,并非是由递推公式求通项公式,而是求某一项或某几项的值,这样对问题的分析思路有所变化,处理上有一定的技巧因此增加了难度;又有分类讨论思想,函数,不等式左右夹逼思想的应用,因此综合性较强.

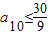 ,同理可得33=a99≤9a10+3a3+11
,同理可得33=a99≤9a10+3a3+11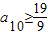 ,即有
,即有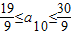 ,又因为an∈Z,所以a10=3.
,又因为an∈Z,所以a10=3.

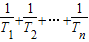 与2的大小;
与2的大小;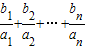 <c恒成立,求整数c的最小值.
<c恒成立,求整数c的最小值.