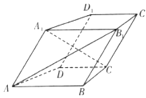
【题目】如图，在四棱柱
中，
，
，
，且
，
.
（1）求证：
；
（2）若四棱柱的体积为
，求直线
与平面
所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）连接
，通过证明
，证得
平面
，由此证得
.
（2）先证得
平面
，由此判断出
是直线
与平面所成角，通过四棱柱
的体积求得四棱柱的高，解三角形求得
.
（1）连接，在四棱柱中，四边形为平行四边形，
∵
，∴四边形为菱形，∴
，
又∵
，
而和
都包含于平面，且
，
所以平面，所以.
（2）∵
，
，
，
∴平面，所以是直线与平面所成角.
因为
，，且
，
，可知四边形
为直角梯形，且为直角腰，取
边中点
，则四边形
为矩形，可求得
，得梯形的面积为
，又因为四棱柱的体积为
，得四棱柱的高为
，
因为平面，得平面
平面，在菱形内作边上的高
，垂足为
，则
平面，
即
.故菱形内
，则
为等边三角形，
，
求得
.（或证明点与点重合，求得
和
，求得）
所以
.
互动课堂系列答案
激活思维智能训练课时导学练系列答案科目：高中数学 来源： 题型：
【题目】微信运动，是由腾讯开发的一个类似计步数据库的公众账号．用户可以通过关注微信运动公众号查看自己每天行走的步数，同时也可以和其他用户进行运动量的
或点赞．微信运动公众号为了解用户的一些情况，在微信运动用户中随机抽取了100名用户，统计了他们某一天的步数，数据整理如下：
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
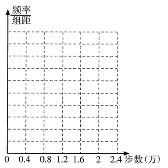
（1）根据表中数据，在如图所示的坐标平面中作出其频率分布直方图，并在纵轴上标明各小长方形的高；
（2）利用分层抽样的方法，从步数在
（万步）中抽取7人，再从这7人中随机抽取2人，求步数在
（万步）的人恰有1人的概率；
（3）这100名用户中，
的用户为男生，这些男生的步数超过1.2万步的人为20人，是否有
的把握认为运动步数超过1.2万步与性别有关？
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，且满足
，
，设
，
.
（Ⅰ）求证：数列
是等比数列；
（Ⅱ）若
，，求实数
的最小值；
（Ⅲ）当
时，给出一个新数列
，其中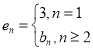
，设这个新数列的前项和为
，若可以写成
（
，
且
，
）的形式，则称为“指数型和”.问
中的项是否存在“指数型和”，若存在，求出所有“指数型和”；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为响应党中央“扶贫攻坚”的号召，某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高，根据以往的经验，随着温度的升高，其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数：
经计算： 
， 
， 
， 
， 
， 
， 
，其中
分别为试验数据中的温度和死亡株数， 
.
（1）若用线性回归模型，求
关于
的回归方程
（结果精确到
）；
（2）若用非线性回归模型求得
关于
的回归方程为
，且相关指数为
.
（i）试与（1）中的回归模型相比，用
说明哪种模型的拟合效果更好；
（ii）用拟合效果好的模型预测温度为
时该批紫甘薯死亡株数（结果取整数）.
附：对于一组数据
， 
，……， 
，其回归直线
的斜率和截距的最小二乘估计分别为： 
；相关指数为： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中，
，
.已知
分别是
的中点.将
沿
折起，使
到
的位置且二面角
的大小是60°，连接
，如图：
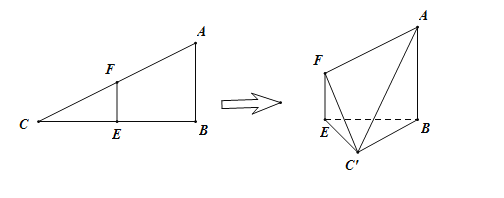
（1）证明：平面
平面
（2）求平面
与平面
所成二面角的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中，底面
是直角梯形，
,
，
,侧面
底面,且
是以
为底的等腰三角形.
（Ⅰ）证明：
（Ⅱ）若四棱锥的体积等于
.问：是否存在过点
的平面
分别交
，
于点
，使得平面
平面
？若存在，求出
的面积；若不存在，请说明理由.
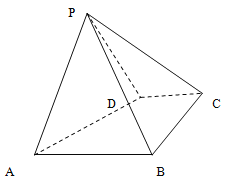
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
