
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余”在18世纪,七巧板流传到了国外,被誉为“东方魔板”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.完整图案为一正方形(如图):五块等腰直角三角形、一块正方形和一块平行四边形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率是( )
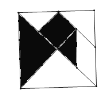
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公比大于0的等比数列{an}中,已知a3a5=a4,且a2,3a4,a3成等差数列.
(1)求{an}的通项公式;
(2)已知Sn=a1a2…an,试问当n为何值时,Sn取得最大值,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知口袋里装有4个大小相同的小球,其中两个标有数字1,两个标有数字2.
(1)从口袋里任意取一球,求取到标有数字2的球的概率;
(2)第一次从口袋里任意取一球,放回口袋里后第二次再任意取一球,记第一次与第二次取到小球上的数字之和为![]() .当
.当![]() 为何值时,其发生的概率最大?说明理由.
为何值时,其发生的概率最大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
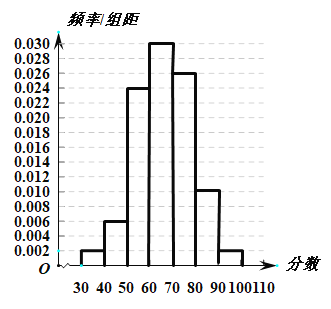
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AB=2CD=2PD=2,PC![]() ,且有PD⊥AD,AD⊥CD,AB∥CD.
,且有PD⊥AD,AD⊥CD,AB∥CD.

(1)证明:PD⊥平面ABCD;
(2)若四棱锥P﹣ABCD的体积为![]() ,求四棱锥P﹣ABCD的表面积.
,求四棱锥P﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com