
【题目】在一次抽奖活动中,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
(1)求![]() 能获一等奖的概率;
能获一等奖的概率;
(2)若![]() ,
,![]() 已获一等奖,求
已获一等奖,求![]() 能获奖的概率.
能获奖的概率.
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
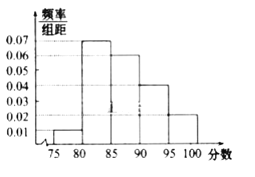
![]() 分别求第
分别求第![]() 组的频率;
组的频率;
![]() 若该校决定在第
若该校决定在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名学生进入第二轮面试,
名学生进入第二轮面试,
![]() 已知学生甲和学生乙的成绩均在第
已知学生甲和学生乙的成绩均在第![]() 组,求学生甲和学生乙同时进入第二轮面试的概率;
组,求学生甲和学生乙同时进入第二轮面试的概率;
![]() 根据直方图试估计这
根据直方图试估计这![]() 名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
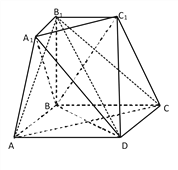
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() .M为CD的中点.
.M为CD的中点.

(1)若点E为PC的中点,求证:BE∥平面PAD;
(2)当平面PBD⊥平面ABCD时,求点A到平面CEM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过点
的焦点重合,过点![]() 与
与![]() 的长轴垂直的直线交
的长轴垂直的直线交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与
与![]() 相切,且与
相切,且与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com