
【题目】如图![]() ,在高为
,在高为![]() 的等腰梯形
的等腰梯形![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,将它沿对称轴
,将它沿对称轴![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图
,如图![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上(不同于
上(不同于![]() ,
,![]() 两点),连接
两点),连接![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.
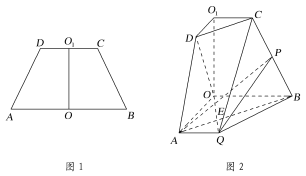
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某避暑山庄拟对一个半径为1百米的圆形地块(如图)进行改造,拟在该地块上修建一个等腰梯形![]() ,其中
,其中![]() ,
,![]() ,圆心
,圆心![]() 在梯形内部,设
在梯形内部,设![]() .当该游泳池的面积与周长之比最大时为“最佳游泳池”.
.当该游泳池的面积与周长之比最大时为“最佳游泳池”.

(1)求梯形游泳池的面积![]() 关于
关于![]() 的函数关系式,并指明定义域;
的函数关系式,并指明定义域;
(2)求当该游泳池为“最佳游泳池”时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(Ⅰ)当![]() ,且直线
,且直线![]()
![]() 轴时, 求四边形
轴时, 求四边形![]() 的面积;
的面积;
(Ⅱ)设![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为左焦点,
为左焦点,![]() 为上顶点,
为上顶点,![]() 为右顶点,若
为右顶点,若![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)是否存在过![]() 点的直线,与
点的直线,与![]() 和
和![]() 交点分别是
交点分别是![]() 和
和![]() ,使得
,使得![]() ?如果存在,求出直线的方程;如果不存在,请说明理由.
?如果存在,求出直线的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线L: y=x+m与抛物线y2=8x交于A、B两点(异于原点),
(1)若直线L过抛物线焦点,求线段 |AB|的长度;
(2)若OA⊥OB ,求m的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com