
【题目】某市为了解本市![]() 万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布
万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
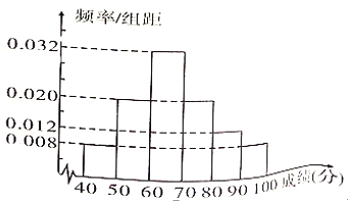
(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)求这![]() 名学生成绩在
名学生成绩在![]() 内的人数;
内的人数;
(3)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:若![]() ,则
,则![]() ,
, ![]()
![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 且
且![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]()
![]() 且
且![]() ,若
,若![]() ,是否存在实数
,是否存在实数![]() 使函数
使函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动规定,一次购物付款总额:
(1)如果标价总额不超过200元,则不给予优惠;
(2)如果标价总额超过200元但不超过500元,则按标价总额给予9折优惠;
(3)如果标价总额超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.
某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.550元B.560元C.570元D.580元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1).在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
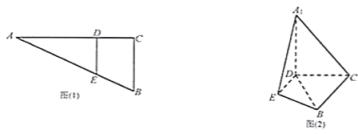
(1)求证:![]() 平面
平面![]() ;
;
(2)当点![]() 在何处时,三棱锥
在何处时,三棱锥![]() 体积最大,并求出最大值;
体积最大,并求出最大值;
(3)当三棱锥![]() 体积最大时,求
体积最大时,求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的数学学习能力,进行了主题分别为“运算”、“推理”、“想象”、“建模”四场竞赛.规定:每场竞赛前三名得分分别为![]() 、
、![]() 、
、![]() (
(![]() ,且
,且![]() 、
、![]() 、
、![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终得分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
分,且乙在“运算”这场竞赛中获得了第一名,那么“运算”这场竞赛的第三名是( )
A.甲B.乙C.丙D.甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆的一个顶点与两个焦点构成的三角形面积为2.
,椭圆的一个顶点与两个焦点构成的三角形面积为2.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与
两点,且与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(i)若![]() ,求
,求![]() 的值;
的值;
(ii)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图), ![]() 为
为![]() 中点.
中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值,并加以证明;若不存在,请说明理由.
的值,并加以证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com