
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
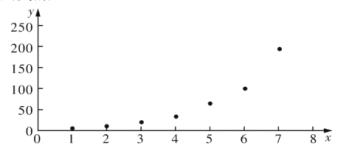
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: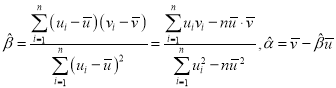 .
.
【答案】(1)![]() 适宜作为扫码支付的人数
适宜作为扫码支付的人数![]() 关子活动推出天数
关子活动推出天数![]() 的回归方程类型;(2)见解析(3)
的回归方程类型;(2)见解析(3)![]() (元).
(元).
【解析】
(1)由于散点图呈指数型增长,则![]() 更适宜;
更适宜;
(2)将非线性的回归方程![]() ,利用对数的运算性质转化为线性的,再利用最小二乘法求解即可得出回归方程,并代值,即可得出第8天使用扫码支付的人次;
,利用对数的运算性质转化为线性的,再利用最小二乘法求解即可得出回归方程,并代值,即可得出第8天使用扫码支付的人次;
(3)分别计算出每个月三种支付方式的收入,即可得出该车队一辆车一年的总收入.
(1)根据散点图判断,![]() 适宜作为扫码支付的人数
适宜作为扫码支付的人数![]() 关子活动推出天数
关子活动推出天数![]() 的回归方程类型.
的回归方程类型.
(2)∵![]() ,两边同时取常用对数得:
,两边同时取常用对数得:![]() ;
;
设![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,
,![]() ,
,
∴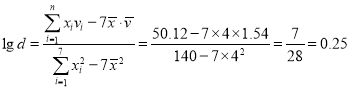 ,
,
把![]() 代入
代入![]() ,得:
,得:![]() ∴
∴![]() ,∴
,∴![]() ,
,
∴![]()
把![]() 代入上式:∴
代入上式:∴![]() ;
;
∴活动推出第8天使用扫码支付的人次为![]() ,
,
∴![]() 关于
关于![]() 的回归方程为,
的回归方程为,![]() ,活动推出第8天使用扫码支付的人次为3470.
,活动推出第8天使用扫码支付的人次为3470.
(3)由题意可知:一个月中使用现金的乘客有1000人,共收入![]() 元;使用乘车卡的乘客有6000人,共收入
元;使用乘车卡的乘客有6000人,共收入![]() 元;
元;
使用扫码支付的乘客有3000人,
其中:享受7折优惠的有500人,共收入![]() 元,
元,
享受8折优惠的有1000人,共收入![]() 元,
元,
享受9折优惠的有1500人,共收入![]() 元,
元,
所以,一辆车一个月的收入为:![]() (元),
(元),
所以,一辆车一年的收入为:![]() (元).
(元).


科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.

若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面正确的是( )
A. m1>m2,s1>s2B. m1>m2,s1<s2
C. m1<m2,s1<s2D. m1<m2,s1>s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与顶点
与顶点![]() 的轨迹交于
的轨迹交于![]() 两点,当线段
两点,当线段![]() 的中点
的中点![]() 落在直线
落在直线![]() 上时,试问:线段
上时,试问:线段![]() 的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆C上一点,以PF1为直径的圆E:x2
1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆C上一点,以PF1为直径的圆E:x2 过点F2.
过点F2.
(1)求椭圆C的方程;
(2)过点P且斜率大于0的直线l1与C的另一个交点为A,与直线x=4的交点为B,过点(3,![]() )且与l1垂直的直线l2与直线x=4交于点D,求△ABD面积的最小值.
)且与l1垂直的直线l2与直线x=4交于点D,求△ABD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示在菱形ABCD中,![]() ,
,![]() ,点E是AD的中点,将
,点E是AD的中点,将![]() 沿BE折起,使得平面
沿BE折起,使得平面![]() 平面BCDE得到如图2所示的四棱锥
平面BCDE得到如图2所示的四棱锥![]() ,点F为AC的中点.在图2中
,点F为AC的中点.在图2中
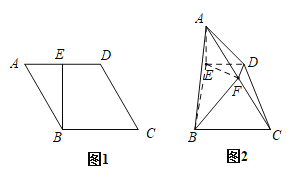
(Ⅰ)证明:![]() 平面ABE;
平面ABE;
(Ⅱ)求点A到平面BEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
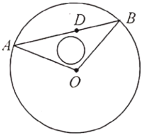
【题目】有一块以点![]() 为圆心,半径为
为圆心,半径为![]() 百米的圆形草坪,草坪内距离
百米的圆形草坪,草坪内距离![]() 点
点![]() 百米的
百米的![]() 点有一用于灌溉的水笼头,现准备过点
点有一用于灌溉的水笼头,现准备过点![]() 修一条笔直小路交草坪圆周于
修一条笔直小路交草坪圆周于![]() 两点,为了方便居民散步,同时修建小路
两点,为了方便居民散步,同时修建小路![]() ,其中小路的宽度忽略不计.
,其中小路的宽度忽略不计.
(1)若要使修建的小路的费用最省,试求小路的最短长度;
(2)若要在![]() 区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和
区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的两个焦点,过
的两个焦点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 在
在![]() 轴上方),则四边形
轴上方),则四边形![]() 面积的最大值为__________.
面积的最大值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com