练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆 （a＞b＞0）与直线x+y=1交于P、Q两点，且OP⊥OQ，其中O为坐标原点．
    （1）求 的值；
    （2）若椭圆的离心率e满足 ≤e≤ ，求椭圆长轴的取值范围．

    【答案】
    （1）解：设P（x1，y1），Q（x2，y2）由OP⊥OQ 可得 x 1x 2+y1 y 2=0

    ∵y1=1﹣x1，y2=1﹣x2

    ∴2x1x2﹣（x1+x2）+1=0①又将y=1﹣x代入 可得（a2+b2）x2﹣2a2x+a2（1﹣b2）=0

    ∵△＞0∴ ，

    代入①化简得 ．


    （2）∵

    ∴

    ∴

    又由（1）知

    ∴ ∴ ，

    ∴长轴 2a∈[ ]．


    【解析】（1）设P（x1，y1），Q（x2，y2）。由P,Q分别在椭圆上，直线上，OP⊥OQ联立方程组即可求出答案。
    （2）由且求出a的范围。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知双曲线过点 且与椭圆 有相同的焦点.
    （1）求双曲线的标准方程；
    （2）若点 在双曲线上， 为左，右焦点，且 ，试求△ 的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是由正整数构成的数表，用aij表示i行第j个数（i，j∈N＋）．此表中ail＝aii＝i，每行中除首尾两数外，其他各数分别等于其“肩膀”上的两数之和．

    （1）写出数表的第六行（从左至右依次列出）．

    （2）设第n行的第二个数为bn（n≥2），求bn．

    （3）令，记Tn为数列前n项和，求的最大值，并求此时n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表是一位母亲给儿子作的成长记录：

    年龄/周岁

    3

    4

    5

    6

    7

    8

    9

    身高/cm

    94.8

    104.2

    108.7

    117.8

    124.3

    130.8

    139.1

    根据以上样本数据，她建立了身高 （cm）与年龄x（周岁）的线性回归方程为 ，给出下列结论：
    ①y与x具有正的线性相关关系；
    ②回归直线过样本的中心点（42，117.1）；
    ③儿子10岁时的身高是 cm；
    ④儿子年龄增加1周岁，身高约增加 cm.
    其中，正确结论的个数是
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆 =1（a＞b＞0），F1 ， F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B．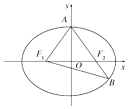

    （1）若∠F1AB=90°，求椭圆的离心率；
    （2）若椭圆的焦距为2，且 =2 ，求椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的前n项和为Sn=a2n+b，且a1=3．
    （1）求a、b的值及数列{an}的通项公式；
    （2）设bn= ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小朋友按如下规则练习数数，大拇指，食指，中指，无名指，小指，无名指，中指，食指，大拇指，食指，，一直数到时，对应的指头是（ ）

    A. 小指 B. 中指 C. 食指 D. 无名指

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在长方体 中， ， ，点 在棱 上移动，则直线 与 所成角的大小是 ， 若 ，则 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，恒成立，求实数m的取值范围；

    （2）是否存在整数a、b（其中a、b是常数，且a＜b），使得关于x的不等式的解集为？若存在，求出a、b的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案