(1)因为f(x)是偶函数,所以f(-x)=f(x)
而当x∈

时,f(x)=sinx,所以x
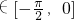
时,

,
f(x)=f(-x)=sin(-x)=-sinx.
又当x
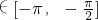
时,x+π∈

,
因为f(x)的周期为π,所以f(x)=f(π+x)=sin(π+x)=-sinx.
所以当x∈[-π,0]时f(x)=-sinx.
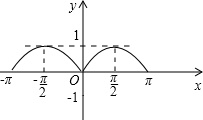
(2)函数图象如图,
(3)由于f(x)的最小正周期为π,
因此先在[-π,0]上来研究
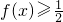
,即
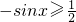
.
所以
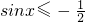
.所以,
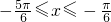
.
由周期性知,当
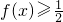
时,

(k∈Z).
所以,当
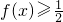
时,x的取值范围是

(k∈Z).
分析:(1)首先取x
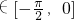
,得到

,把-x代入

时的解析式,结合偶函数的概念可求得
x
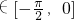
时的解析式,然后再取x
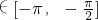
,加π后得到x+π∈

,代入

时的解析式,
结合周期函数的概念求解f(x);
(2)作出函数在[-π,0]上的图象,根据偶函数图象关于y轴轴对称得到函数在[0,π]上的图象;
(3)先求出[-π,0]上满足
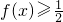
的x的取值范围,根据函数是以π为周期的周期函数,把得到的区间端点值加上π的整数倍得到要求解的区间.
点评:本题考查了函数解析式的求解及常用方法,考查了三角函数的周期及图象,考查了三角函数的奇偶性,解答此题的关键是,通过周期变换和平移变换、把要求解解析式的范围内的变量转化到已知解析式的范围内,此题是中档题.

 时,f(x)=sinx
时,f(x)=sinx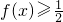 时,x的取值范围.
时,x的取值范围. 时,f(x)=sinx,所以x
时,f(x)=sinx,所以x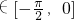 时,
时, ,
,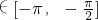 时,x+π∈
时,x+π∈ ,
,
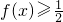 ,即
,即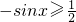 .
.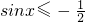 .所以,
.所以,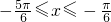 .
.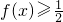 时,
时, (k∈Z).
(k∈Z).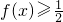 时,x的取值范围是
时,x的取值范围是 (k∈Z).
(k∈Z).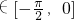 ,得到
,得到 ,把-x代入
,把-x代入 时的解析式,结合偶函数的概念可求得
时的解析式,结合偶函数的概念可求得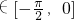 时的解析式,然后再取x
时的解析式,然后再取x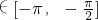 ,加π后得到x+π∈
,加π后得到x+π∈ ,代入
,代入 时的解析式,
时的解析式,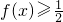 的x的取值范围,根据函数是以π为周期的周期函数,把得到的区间端点值加上π的整数倍得到要求解的区间.
的x的取值范围,根据函数是以π为周期的周期函数,把得到的区间端点值加上π的整数倍得到要求解的区间.

 阅读快车系列答案
阅读快车系列答案