
【题目】设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
(1)求函数f(x)的解析式;
(2)求g(x)=f(3x+![]() )﹣1在[﹣
)﹣1在[﹣![]() ,
, ![]() ]上的值域.
]上的值域.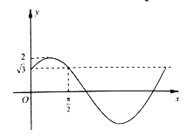
【答案】解:(1)由图形可得:A=2,…2分
将点(0,![]() ),(
),(![]() ,
,![]() )代入,有φ
)代入,有φ ,
,
∵0<|φ|<π,
∴![]() ,
,
故f(x)=2sin(![]() +
+![]() ).
).
(2)g(x)=f(3x+![]() )﹣1=2sin[
)﹣1=2sin[![]() (3x+
(3x+![]() )+
)+![]() ]﹣1
]﹣1
=2sin(2x+![]() )﹣1=2cos2x﹣1,
)﹣1=2cos2x﹣1,
当x∈[﹣![]() ,
,![]() ]时,2x∈[﹣
]时,2x∈[﹣![]() ,
,![]() ],cos2x∈[﹣
],cos2x∈[﹣![]() ,1],
,1],
故g(x)=f(3x+![]() )﹣1在∈[﹣
)﹣1在∈[﹣![]() ,
,![]() ]上的值域为:[﹣2,1]
]上的值域为:[﹣2,1]
【解析】(1)由函数的图象的顶点坐标求出A,由特殊点的坐标求出φ的值,再根据五点法作图求出ω的值,从而求得该函数的解析式.
(2)利用三角函数恒等变换的应用先求函数解析式g(x)=2cos2x﹣1,由x∈[﹣![]() ,
, ![]() ],利用余弦函数的图形和性质即可得解其值域.
],利用余弦函数的图形和性质即可得解其值域.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ ![]() )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a2=2,前n项和为 ![]() . (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
. (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,数列{bn}的前n项和为Tn , 求使不等式
,数列{bn}的前n项和为Tn , 求使不等式 ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
A.a>b>c
B.b>c>a
C.c>a>b
D.c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条不重合的直线 ![]() 和两个不重合的平面
和两个不重合的平面 ![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(﹣1,1)上的增函数f(x)= ![]() 为奇函数,且f(
为奇函数,且f( ![]() )=
)= ![]()
(1)求函数f(x)的解析式;
(2)解关于t的不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com