练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元.该公司第年需要付出设备的维修和工人工资等费用的信息如下图 .

    （1）求；

    （2）引进这种设备后，第几年后该公司开始获利；

    （3）这种设备使用多少年，该公司的年平均获利最大？

    【答案】（1）；（2）；（3）.

    【解析】

    试题分析：（1）由图可知，每年费用是以为首项，为公差的等差数列，所以；（2）设纯收入与年数的关系为，则：，由解得，点的最小值为；（3）年平均收入为，当且仅当即时等号成立.

    试题解析：

    （1）由题意知，每年费用是以2为首项，2为公差的等差数列，求得：

    （2）设纯收入与年数的关系为，则：

    由各，解得

    又因为，所以，即从第2年该公司开始获利

    （3）年平均收入为

    当且仅当时，年平均收益最大，

    所以这种设备使用5年，该公司的年平均获利最大

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】机床厂今年年初用98万元购进一台数控机床，并立即投入生产使用，计划第一年维修、保养费用12万元，从第二年开始，每年所需维修、保养费用比上一年增加4万元，该机床使用后，每年的总收入为50万元，设使用x年后数控机床的盈利额为y万元．

    (Ⅰ)写出y与x之间的函数关系式；

    (Ⅱ)从第几年开始，该机床开始盈利（盈利额为正值）；

    (Ⅲ)使用若干年后，对机床的处理方案有两种：

    (1)当年平均盈利额达到最大值时，以30万元价格处理该机床；

    (2)当盈利额达到最大值时，以12万元价格处理该机床．

    请你研究一下哪种方案处理较为合理？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ax2－2x＋1.

    （1）当,试讨论函数f（x）的单调性；

    （2）若≤a≤1，且f（x）在[1,3]上的最大值为M（a），最小值为N（a），令g（a）＝M（a）－N（a），求g（a）的表达式；

    （3）在（2）的条件下，求g（a）的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时，则视为合格品，否则视为不合格品.在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差（单位：mm），将所得数据分组，得到如下频率分布表：

    （1）将上面表格中缺少的数据填在相应位置上；

    （2）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；

    （3）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品.据此估算这批产品中的合格品的件数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的两个焦点与短轴的一个端点是等边三角形的三个顶点，且长轴长为4.

    （1）求椭圆的方程；

    （2）若是椭圆的左顶点，经过左焦点的直线与椭圆交于，两点，求与的面积之差的绝对值的最大值.（为坐标原点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.圆锥的底面是圆面，侧面是曲面

    B.用一张扇形的纸片可以卷成一个圆锥

    C.一个物体上、下两个面是相等的圆面，那么它一定是一个圆柱

    D.圆台的任意两条母线的延长线可能相交也可能不相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学为了了解全校学生的上网情况，在全校采用随机抽样的方法抽取了40名学生（其中男女生人数恰好各占一半）进行问卷调查，并进行了统计，按男女分为两组，再将每组学生的月上网次数分为5组：，，，，，得到如图所示的频率分布直方图：

    （1）写出的值；

    （2）求抽取的40名学生中月上网次数不少于15次的学生人数；

    （Ⅲ）在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人 ，求至少抽到1名女生的概率.

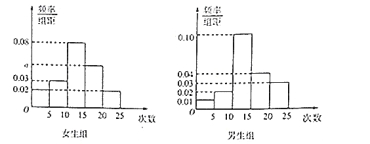
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（1），在三角形中，为其中位线，且，若沿将三角形折起，使，构成四棱锥，且．

    （1）求证：平面 平面；

    （2）当 异面直线与所成的角为时，求折起的角度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】脱贫是政府关注民生的重要任务，了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取个农户，考察每个农户的年收入与年积蓄的情况进行分析，设第个农户的年收入（万元），年积蓄（万元），经过数据处理得

    （Ⅰ）已知家庭的年结余对年收入具有线性相关关系，求线性回归方程；

    （Ⅱ）若该地区的农户年积蓄在万以上，即称该农户已达小康生活，请预测农户达到小康生活的最低年收入应为多少万元？

    附：在 中， 其中为样本平均值.

    查看答案和解析>>

    同步练习册答案